
【题目】定义: 对于平面直角坐标系xOy上的点P(a, b) 和抛物线![]() , 我们称P(a, b)是抛物线
, 我们称P(a, b)是抛物线![]() 的相伴点, 抛物线
的相伴点, 抛物线![]() 是点P(a, b) 的相伴抛物线.
是点P(a, b) 的相伴抛物线.
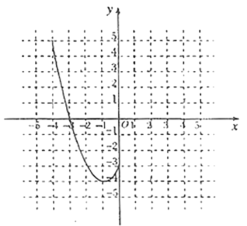
如图,已知点A(-2, -2),B(4, -2),C(1, 4).
(1) 点A的相伴抛物线的解析式为 ;过A, B两点的抛物线![]() 的相伴点坐标为 ;
的相伴点坐标为 ;
(2) 设点P(a, b) 在直线AC上运动:
①点P(a, b)的相伴抛物线的顶点都在同一条抛物线Ω上, 求抛物线Ω的解析式.
②当点P(a, b)的相伴抛物线的顶点落在△ABC 内部时, 请直接写出 a 的取值范围.
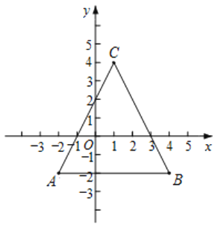
【答案】(1)y=x2-2x-2;P(-2,-10);(2)①y=-x2-4x+2;②![]() .
.
【解析】
(1)a=b=﹣2,故抛物线的表达式为:y=x2﹣2x﹣2.
故答案为:y=x2﹣2x﹣2;将点A、B坐标代入y=x2+ax+b并解得:a=﹣2,b=﹣10;
(2)①直线AC的表达式为:y=2x+2,设点P(m,2m+2),则抛物线的表达式为:y=x2+mx+2m+2,顶点为:(![]() m,
m,![]() m2+2m+2),即可求解;
m2+2m+2),即可求解;
②如图所示,Ω抛物线落在△ABC内部为EF段,即可求解.
(1)a=b=﹣2,故抛物线的表达式为:y=x2﹣2x﹣2.
故答案为:y=x2﹣2x﹣2;
将点A、B坐标代入y=x2+ax+b得:![]() ,解得:a=﹣2,b=﹣10.
,解得:a=﹣2,b=﹣10.
故答案为:(﹣2,﹣10);
(2)①由点A、C的坐标得:直线AC的表达式为:y=2x+2,
设点P(m,2m+2),则抛物线的表达式为:y=x2+mx+2m+2,
顶点为:(![]() m,
m,![]() m2+2m+2),
m2+2m+2),
令x![]() m,则m=﹣2x,
m,则m=﹣2x,
则y![]() m2+2m+2=﹣x2﹣4x+2,
m2+2m+2=﹣x2﹣4x+2,
即抛物线Ω的解析式为:y=﹣x2﹣4x+2;
②如图所示,Ω抛物线落在△ABC内部为EF段,

抛物线与直线AC的交点为点E(0,2);
当y=﹣2时,即y=﹣x2﹣4x+2=﹣2,解得:x=﹣2![]() ,
,
故点F(﹣2![]() ,﹣2);
,﹣2);
故0<x<﹣2+2![]() ,由①知:a=m=﹣2x,
,由①知:a=m=﹣2x,
故:4﹣4![]() a<0.
a<0.


科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上动点,以
上动点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 所在直线与
所在直线与![]() 所在直线交于点
所在直线交于点![]() ,连接
,连接![]() .
.
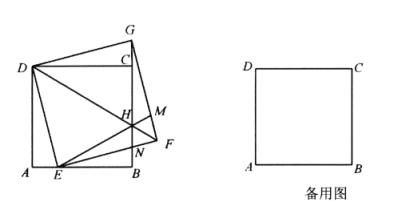
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②若![]() ,求
,求![]() 的值;
的值;
(2)当正方形![]() 的边长为4,
的边长为4,![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
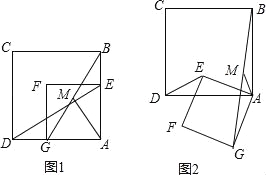
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在等边△ABC中, D, E, F分别为边AB, BC, CA上的点, 且满足∠DEF=60°.
(1)求证:![]() ;
;
(2)若DE⊥BC且DE=EF, 求![]() 的值.
的值.
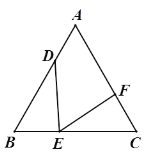
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢,设计图案如图所示(四周是四个全等的矩形,用材料甲进行装潢;中心区是正方形MNPQ,用材料乙进行装潢).

两种装潢材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,装潢材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1760元购买材料一定够用吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ________________.
________________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分;
(3)观察函数图像,写出两条函数的性质;
(4)进一步探究函数图像发现:
①方程![]() 有______个实数根;
有______个实数根;
②函数图像与直线![]() 有_______个交点,所以对应方程
有_______个交点,所以对应方程![]() 有_____个实数根;
有_____个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)

请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com