
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 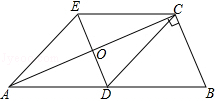
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
【答案】
(1)证明:∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形ADCE是菱形
(2)解:Rt△ABC中,CD为AB边上的中线,∠B=60°,BC=6,
∴AD=DB=CD=6.
∴AB=12,由勾股定理得 ![]() .
.
∵四边形DBCE是平行四边形,
∴DE=BC=6.
∴ ![]()
【解析】(1)欲证明四边形ADCE是菱形,需先证明四边形ADCE为平行四边形,然后再证明其对角线相互垂直;(2)根据勾股定理得到AC的长度,由含30度角的直角三角形的性质求得DE的长度,然后由菱形的面积公式:S= ![]() ACDE进行解答.
ACDE进行解答.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A. 3:4:3:4 B. 5:2:2:5 C. 2:3:4:5 D. 3:3:4:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C、D不重合).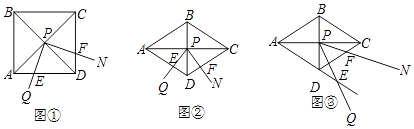
(1)如图①,当α=90°时,求证:DE+DF=AD.
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为 ![]() ,请给出证明.
,请给出证明.
(3)在(2)的条件下,将∠QPN绕点P旋转,若旋转过程中∠QPN的边PQ与边AD的延长线交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
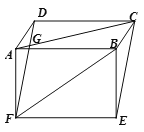
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com