
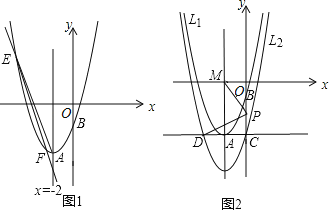
【题目】抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为![]() ,求k的值;
,求k的值;
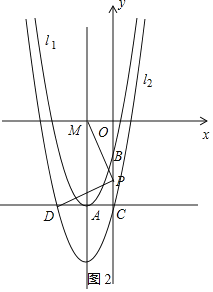
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
【答案】(1)y=x2+4x﹣2;(2)k=﹣4;(3)当n=4![]() ﹣2时,点P的坐标为(0,﹣2
﹣2时,点P的坐标为(0,﹣2![]() )和(0,﹣
)和(0,﹣![]() );当n=4时,点P坐标为(0,﹣2)和(0,﹣4).
);当n=4时,点P坐标为(0,﹣2)和(0,﹣4).
【解析】
(1)待定系数法求解可得;
(2)设直线y=kx+2k-8与抛物线l1的对称轴交点为G,则G(-2,-8),由顶点A坐标知AG=2,由S△AEF=S△AGE-S△AGF=![]() AG(-2-xE)-
AG(-2-xE)-![]() AG(-2-xF)=
AG(-2-xF)=![]() AG(xF-xE)=2
AG(xF-xE)=2![]() 知xF-xE=2
知xF-xE=2![]() ,再联立得
,再联立得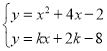 ,消去y整理得x2+(4-k)x-2k+6=0,据此知
,消去y整理得x2+(4-k)x-2k+6=0,据此知![]() ,继而得出xF-xE=
,继而得出xF-xE=![]() ,据此可得关于k的方程,解之可得答案;
,据此可得关于k的方程,解之可得答案;
(3)分△PCD∽△MOP和△PCD∽△POM得出t关于n的关系式,再根据符合该条件的点P有且只有两个,进一步求解可得.
解:(1)∵y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2)
∴可得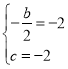 ,解得
,解得![]() ,
,
∴抛物线l1的解析式为y=x2+4x﹣2.
(2)如图1,设直线y=kx+2k﹣8与抛物线l1的对称轴交点为G,则G(﹣2,﹣8),
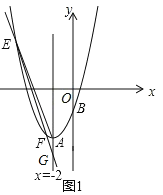
又可得抛物线l1的顶点A(﹣2,﹣6),
∴AG=2,
S△AEF=S△AGE﹣S△AGF
![]()
![]()
又∵S△AEF=2![]() ,AG=2,
,AG=2,
∴xF﹣xE=2![]() ,
,
将抛物线l1与直线y=kx+2k﹣8联立得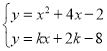 ,
,
消去y得x2+4x﹣2=kx+2k﹣8,
整理得x2+(4﹣k)x﹣2k+6=0,得![]() ,
,
∴xF﹣xE=![]() ,
,
∴![]() ,
,
解得k=±4,
又k<0,
∴k=﹣4.
(3)设抛物线l2的解析式为y=x2+4x﹣2﹣m,
∴C(0,﹣2﹣n),D(﹣4,﹣2﹣n),M(﹣2,0)
设P(0,t).
①当△PCD∽△MOP时,![]() ,
,
∴![]() ,
,
∴t2+(n+2)t+8=0;
②当△PCD∽△POM时,![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
(Ⅰ)当方程①有两个相等实数根时,
△=(n+2)2﹣4×1×8=0,
解得n=±4![]() ﹣2,
﹣2,
又n>0,
∴n=4![]() ﹣2,
﹣2,
此时方程①有两个相等实根t1=t2=﹣2![]() ,方程②有一个实数根t=
,方程②有一个实数根t=![]() ;
;
∴n=4![]() ﹣2,
﹣2,
此时点P的坐标为(0,﹣2![]() )和(0,
)和(0,![]() );
);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:![]() ,即(n+2)2=36,
,即(n+2)2=36,
解得n1=4,n2=﹣8,
又n>0,
∴n=4,
此时方程①有两个不相等的实数根,t1=﹣2,t2=﹣4,方程①有一个实数根t=﹣2;
∴n=4,
此时点P坐标为(0,﹣2)和(0,﹣4),
综上,当n=4![]() ﹣2时,点P的坐标为(0,﹣2
﹣2时,点P的坐标为(0,﹣2![]() )和(0,
)和(0,![]() );当n=4时,点P坐标为(0,﹣2)和(0,﹣4).
);当n=4时,点P坐标为(0,﹣2)和(0,﹣4).


科目:初中数学 来源: 题型:
【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
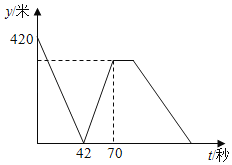
【题目】国防教育和素质拓展期间,某天小明和小亮分别从校园某条路的A,B两端同时相向出发,当小明和小亮第一次相遇时,小明觉得自己的速度太慢便决定提速至原速的![]() 倍,当他到达B端后原地休息,小亮匀速到达A端后,立即按照原速返回B端(忽略掉头时间).两人相距的路程y(米)与小亮出发时间t(秒)之间的关系如图所示,当小明到达B端后,经过_____秒,小亮回到B端.
倍,当他到达B端后原地休息,小亮匀速到达A端后,立即按照原速返回B端(忽略掉头时间).两人相距的路程y(米)与小亮出发时间t(秒)之间的关系如图所示,当小明到达B端后,经过_____秒,小亮回到B端.
查看答案和解析>>
科目:初中数学 来源: 题型:
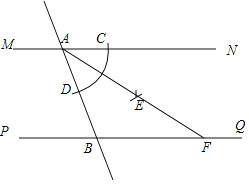
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用以下步骤作图:
①以点A为圆心,适当长为半径作弧交射线AN于点C,交线段AB于点D;
②以点C为圆心,适当长为半径画弧;然后再以点D为圆心,同样长为半径画弧.前后两弧在∠NAB内交于点E;
③作射线AE,交PQ于点F;
若AF=2![]() ,∠FAN=30°,则线段BF的长为_____.
,∠FAN=30°,则线段BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是弧
是弧![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() .连接
.连接![]() ,关于下列结论:①
,关于下列结论:①![]()
![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心,其中正确结论是( )
的外心,其中正确结论是( )
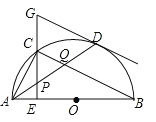
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.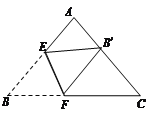
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com