
| A. | 0 | B. | 1 | C. | 2 | D. | 3 | ||||
| E. | 4 |
分析 根据x是无理数,且(x+1)(x+3)是有理数,得出x2+4x+3是有理数,再将选项中各式变形,再利用有理数与无理数的性质得出即可.
解答 解:x是无理数,且(x+1)(x+3)=x2+4x+3,是有理数,
(1)x2是有理数,则x2+4x+3为无理数,矛盾,故此选项错误;
(2)(x-1)(x-3)=(x2+4x+3)-8x,而有理数减无理数仍为无理数,故此选项正确,
(3)(x+1)2=(x2+4x+3)-2x-2是无理数;故此选项错误;
(4)(x-1)2=(x2+4x+3)-6x-2是无理数;故此选项正确;
∴正确的有:2个.
故选C.
点评 此题主要考查了有理数与无理数的概念与运算,根据已知得出x2+4x+3是有理数再将选项各式使其出现x2+4x+3是解题关键.


科目:初中数学 来源: 题型:选择题
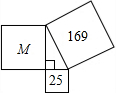 如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )| A. | 12 | B. | 13 | C. | 144 | D. | 194 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对P有无限多个位置,使得S<2CP2 | |
| B. | 对P有有限多个位置,使得S<2CP2 | |
| C. | 当且仅当P为AB的中点,或者P与顶点A,B之一有重合时,才有S=2CP2 | |
| D. | 对直线AB上的所有点P,总有S=2CP2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a>-b | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a+m<b+m | D. | a2>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com