
| A. | $\frac{25}{2}$mm | B. | $\frac{25}{2}$$\sqrt{3}$mm | C. | $\frac{25}{4}$mm | D. | $\frac{25}{4}$$\sqrt{3}$mm |
分析 根据题意得出圆内接半径r为$\frac{25}{2}$mm,求出OB,得出BD=OB•sin30°,则BC=2BD,即可得出结果.
解答 解:根据题意得:圆内接半径r为$\frac{25}{2}$mm,如图所示: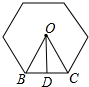
则OB=$\frac{25}{2}$,
∴BD=OB•sin30°=$\frac{25}{2}$×$\frac{1}{2}$=$\frac{25}{4}$(mm),
则BC=2×$\frac{25}{4}$=$\frac{25}{2}$(cm),
完全覆盖住的正六边形的边长最大为$\frac{25}{2}$mm.
故选:A.
点评 本题考查了正多边形和圆、正六边形的性质、三角函数、等腰三角形的性质等知识;运用三角函数求出圆内接正六边形的边长是解决问题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,
如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)
如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?($\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$>\frac{1}{2}$ | B. | -1$≤x<\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x≥-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
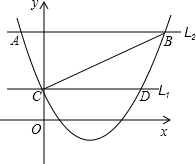 如图,抛物线F:y=ax2+bx+c(a>0)与y轴相交于点C,直线L1经过点C且平行于x轴,将L1向上平移t(t>0)个单位得到直线L2.设L1与抛物线F的交点为C、D,L2与抛物线F的交点为A、B,连结AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴相交于点C,直线L1经过点C且平行于x轴,将L1向上平移t(t>0)个单位得到直线L2.设L1与抛物线F的交点为C、D,L2与抛物线F的交点为A、B,连结AC、BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为4.
如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com