
分析 根据二次根式中的被开方数必须是非负数,以及平方根、立方根的含义和求法求解即可.
解答 解:∵$\sqrt{2x-1}{+^3}\sqrt{1-x}$有意义,
∴2x-1≥0,
∴x的取值范围是x≥$\frac{1}{2}$;
4的平方根是:±$\sqrt{4}$=±2;
-27的立方根是:$\root{3}{-27}$=-3;
∵$\root{3}{8}=2$,
∴$\root{3}{8}$的平方根是:±$\sqrt{2}$;
∵$\sqrt{64}$=8,
∴-$\sqrt{64}$的立方根是:$\root{3}{-8}$=-2.
故答案为:x≥$\frac{1}{2}$;±2;-3;±$\sqrt{2}$;-2.
点评 此题主要考查了二次根式有意义的条件,平方根、立方根的含义和求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
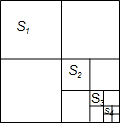 【阅读】求值:1+2+22+23+…+22016
【阅读】求值:1+2+22+23+…+22016查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E、F分别是矩形ABCD的边AD、AB上的点,EF=EC,且EF⊥EC.
如图,E、F分别是矩形ABCD的边AD、AB上的点,EF=EC,且EF⊥EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A在∠B的边BG上,AB=5,sin∠B=$\frac{3}{5}$,点P是∠B的边BH上任意一点,连接AP,以AP为直径画⊙O交BH于C点. 若BP=$\frac{25}{4}$,求证:BG与⊙O相切.
如图,点A在∠B的边BG上,AB=5,sin∠B=$\frac{3}{5}$,点P是∠B的边BH上任意一点,连接AP,以AP为直径画⊙O交BH于C点. 若BP=$\frac{25}{4}$,求证:BG与⊙O相切.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正整数和负整数统称为整数 | B. | 有理数都可以用数轴上的点来表示 | ||
| C. | 符号不同的两个数叫做互为相反数 | D. | 两个有理数,绝对值大的反而小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在13×6的正方形网格中(每个小正方形的边长均为1)有线段AB,点A、B均在正方形的顶点上.
如图,在13×6的正方形网格中(每个小正方形的边长均为1)有线段AB,点A、B均在正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com