
【题目】如图,抛物线y= ![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣ ![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】解:(1)把A(0,3),C(3,0)代入y= ![]() x2+mx+n,得
x2+mx+n,得
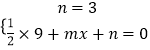 ,
,
解得: 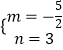 .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+3.
x+3.
联立 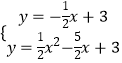 ,
,
解得: ![]() 或
或 ![]() ,
,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
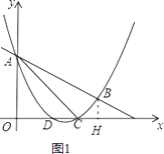
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC= ![]() .
.
同理:∠ACO=45°,AC=3 ![]() ,
,
∴∠ACB=180°﹣45°﹣45°=90°,
∴tan∠BAC= ![]() ;
;
(2)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,
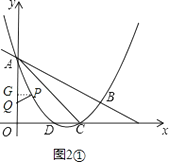
则∠PGA=90°.
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,
∴ ![]() .
.
∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y= ![]() x2﹣
x2﹣ ![]() x+3,得:
x+3,得: ![]() x2﹣
x2﹣ ![]() x+3=3﹣3x,
x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
②如图2②,
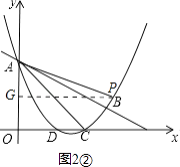
当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:AG= ![]() PG=
PG= ![]() x,则P(x,3﹣
x,则P(x,3﹣ ![]() x),
x),
把P(x,3﹣ ![]() x)代入y=
x)代入y= ![]() x2﹣
x2﹣ ![]() x+3,得:
x+3,得: ![]() x2﹣
x2﹣ ![]() x+3=3﹣
x+3=3﹣ ![]() x,
x,
整理得:x2﹣ ![]() x=0,解得:x1=0(舍去),x2=
x=0,解得:x1=0(舍去),x2= ![]() ,∴P(
,∴P( ![]() ,
, ![]() );
);
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P( ![]() ,
, ![]() ).
).
综上所述:满足条件的点P的坐标为(11,36)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() ).
).
【解析】(1)将点A、B的坐标代入抛物线的解析式得到关于m、n的方程组,从而可求得m、n;过点B作BH⊥OH,先求得点C的坐标,然后再证明△AOC和△BHC为等腰直角三角形,从而可求得∠ACB=90°,然后依据勾股定理可求得AC、BC的长,最后依据锐角三角函数的定义可求得答案。
(2)过点P作PG⊥OA,当G在点A的下方时,分为∠PAQ=∠CAB和∠PAQ=∠CBA两种情况,当点G在点A的上方,分为∠PAQ=∠CAB和∠PAQ=∠CBA两情况分类计算即可..
【考点精析】通过灵活运用二次函数图象的平移和相似三角形的判定与性质,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2﹣(m+3)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE![]() AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.
AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形铁皮AOB中,OA=20,AOB=36°,OB在直线 ![]() 上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第一次落在l上时,停止旋转.则点O所经过的路线长为
上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第一次落在l上时,停止旋转.则点O所经过的路线长为 ( )
( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: ![]() ≈1.41).
≈1.41).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com