

分析 (1)根据抛物线y=x2+bx+c过点A(2,0),点B(-1,0),根据待定系数法可求抛物线的解析式;
(2)分三种情况:当以AM为直径的⊙P与直线OC相切时,直线OC上存在点D(即切点),使∠ADM=90°;当⊙P与OC相交时,存在点D(即交点);当⊙P与OC相离时,不存在.如图,设⊙P与OC相切于点Q,连结PQ.根据勾股定理得到关于m的方程,解方程即可得到m的取值范围;
(3)如图,连结MN交直线OC于点E,过点N作NF⊥OM于点F.根据三角函数和三角形面积公式,由对称性可知,当m>0时,点N在第一象限;当m<0时,点N在第三象限;得到点N的坐标为($\frac{3}{5}$m,$\frac{4}{5}$m),把N($\frac{3}{5}$m,$\frac{4}{5}$m)代入y=x2-x-2中,得到关于m的方程,解方程即可求解.
解答 解:(1)∵抛物线y=x2+bx+c过点A(2,0),点B(-1,0),
∴$\left\{\begin{array}{l}{4+2b+c=0}\\{1-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-1}\\{c=-2}\end{array}\right.$.
故抛物线的解析式为y=x2-x-2;
(2)当以AM为直径的⊙P与直线OC相切时,直线OC上存在点D(即切点),使∠ADM=90°,
当⊙P与OC相交时,存在点D(即交点);当⊙P与OC相离时,不存在. 如图,设⊙P与OC相切于点Q,连结PQ.
如图,设⊙P与OC相切于点Q,连结PQ.
则PQ=$\frac{1}{2}$AM=$\frac{1}{2}$|2-m|,
∴OQ=$\frac{PQ}{tan∠AOC}$=|2-m|,OP=|2-$\frac{2-m}{2}$|=$\frac{1}{2}$|2+m|.
∵OQ2+PQ2=OP2,
∴(2-m)2+[$\frac{1}{2}$(2-m)]2=[$\frac{1}{2}$(2+m)]2,
化简得m2-6m+4=0,
解得m1=3-$\sqrt{5}$,m2=3+$\sqrt{5}$.
∴当m≤3-$\sqrt{5}$或m≥3+$\sqrt{5}$时,直线OC上存在点D,使∠ADM=90°. (3)如图,连结MN交直线OC于点E,过点N作NF⊥OM于点F.
(3)如图,连结MN交直线OC于点E,过点N作NF⊥OM于点F.
∵tan$∠AOC=\frac{1}{2}$=$\frac{EM}{OE}$,
∴OE=2EM.
∵OE2+EM2=OM2,
∴4EM2+EM2=m2,
∴EM=$\frac{\sqrt{5}}{5}$|m|.
∴OE=$\frac{2\sqrt{5}}{5}$|m|,MN=2EM=$\frac{2\sqrt{5}}{5}$|m|,
∵OM•NF=MN•OE,
∴NF=$\frac{\frac{2\sqrt{5}}{5}|m|•\frac{2\sqrt{5}}{5}|m|}{|m|}$=$\frac{4}{5}$|m|.
由对称性可知,当m>0时,点N在第一象限;当m<0时,点N在第三象限;
∴点N的坐标为($\frac{3}{5}$m,$\frac{4}{5}$m),
把N($\frac{3}{5}$m,$\frac{4}{5}$m)代入y=x2-x-2中,得$\frac{9}{25}$m2-$\frac{3}{5}$m-2=$\frac{4}{5}$m,
化简得9m2-35m-50=0,
解得m1=-$\frac{10}{9}$,m2=5.
综上所述,M的坐标为(-$\frac{10}{9}$,0)或(5,0).
点评 考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,直线与圆的位置关系,勾股定理,三角函数和三角形面积公式,对称性,分类思想和方程思想的应用,综合性较强,难度较大.


科目:初中数学 来源: 题型:填空题
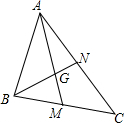 如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
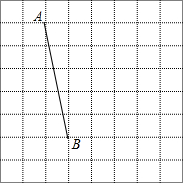 如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.
如图,将线段AB放在每个小正方形的边长为1的网格中,点A,点B均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com