
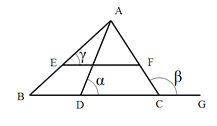
【题目】如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC=3∠BAD,记∠ADC=![]() ,∠ACG=
,∠ACG=![]() ,∠AEF=
,∠AEF=![]() ,则:(1)
,则:(1)![]() __
__![]() (填“>”、“=”或“<”号);
(填“>”、“=”或“<”号);
(2)![]() 、
、![]() 、
、![]() 三者间的数量关系式是_______________.
三者间的数量关系式是_______________.
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】随着我国经济的高速发展,有着“经济晴雨表”之称的股市也得到迅速的发展,下表是今年上证指数某一周星期一至星期五的变化情况. (注:上周五收盘时上证指数为2616点,每一天收盘时指数与前一天相比,涨记为“+”,跌记为“-”)
星 期 | 一 | 二 | 三 | 四 | 五 |
指数的变化(与前一天比较) |
|
|
|
|
|
⑴ 请求出这一周星期五收盘时的上证指数是多少点?
⑵ 说出这一周每一天收盘时上证指数哪一天最高?哪一天最低?分别是多少点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D,E分别在边AB, BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为( )。

A. 70°B. 75°C. 80°D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元宵节将至,我校组织学生制作并选送50盏花灯,共包括传统花灯、创意花灯和现代花灯三大种.已知每盏传统花灯需要35元材料费,每盏创意花灯需要33元材料费,每盏现代花灯需要30元材料费.
(1)如果我校选送20盏现代花灯,已知传统花灯数量不少于5盏且总材料费不得超过1605元,请问选送传统花灯、创意花灯的数量有哪几种方案?
(2)当三种花灯材料总费用为1535元时,求选送传统花灯、创意花灯、现代花灯各几盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC中,AB=AC,∠BAC=90°,过点B,点C分别作经过点A的直线l的垂线,垂足分别为M、N.
(1)请找到一对全等三角形,并说明理由;
(2)BM,CN,MN之间有何数量关系?并说明理由;
(3)若BM=3,CN=5,求四边形MNCB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com