
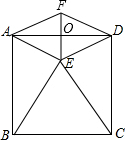
 如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.分析 (1)由正方形和等边三角形的性质得出∠ABE=30°,AB=BE,由等腰三角形的性质和三角形内角和定理即可求出∠AEB的度数;
(2)先判断出△ABE≌△DCE,得到AE=ED,再由翻折的性质即可得出结论;
(3)先由等边三角形的性质求出EH,进而得出OE,借助(2)的结论即可求出EF.
解答 解:(1)∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∵△EBC是等边三角形,
∴BE=BC,∠EBC=60°,
∴∠ABE=90°-60°=30°,AB=BE,
∴∠AEB=∠BAE=$\frac{1}{2}$(180°-30°)=75°;
故答案为75°;
(2)∵四边形ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=CD,
∵△BCE为等边三角形,
∴∠BCE=∠EBC=60°,BE=EC,
∴∠ABE=∠DCE=90°-60°=30°,
∴△ABE≌△DCE,
∴AE=ED,
∵△AED沿着AD翻折为△AFD,
∴AE=ED=AF=FD,
∴四边形AEDF是菱形;
(3)如图,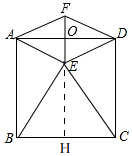
由翻折知,AE=AF,∠FAO=∠EAO,
∴EF⊥AD,过点E作EH⊥BC于H,
在等边三角形BCE中,BC=2,
∴EH=$\frac{\sqrt{3}}{2}$BC=$\sqrt{3}$,
∴EO=OH-EH=AB-EH=2-$\sqrt{3}$,
∴EF=2EO=2(2-$\sqrt{3}$)=4-2$\sqrt{3}$.
点评 此题是四边形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,翻折性质,菱形的判定和性质,解(2)的关键是判断出AE=ED,解(3)的关键是作出辅助线求出EH.是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).
现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
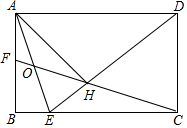 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (2)(4) | D. | (1)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com