
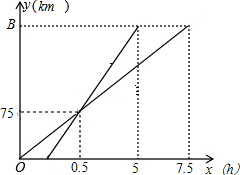
 列慢车和一列快车沿相同的路线从A地到B地,所走的路程y(km)与时间x(h)的函数图象如图所示,试根据图象回答下列问题:
列慢车和一列快车沿相同的路线从A地到B地,所走的路程y(km)与时间x(h)的函数图象如图所示,试根据图象回答下列问题:分析 (1)根据横纵坐标的意义,分别分析得出即可.
(2)由(1)知,两地之间的距离是1125km,根据速度=$\frac{路程}{时间}$来计算快车与慢车的速度;
(3)需要分类讨论:慢车没有出发;慢车已经出发且快车没有到达目的地;快车已到目的地.
解答  解:设慢车从A地到B地,所走的路程y(km)与时间x(h)的函数关系式为y=kx(k≠0),
解:设慢车从A地到B地,所走的路程y(km)与时间x(h)的函数关系式为y=kx(k≠0),
把(0.5,75)代入得,75=0.5k,解得k=150,
∴y=150x,
把x=7.5代入得,y=1125,
∴OB=1125,
设快车从A地到B地,所走的路程y(km)与时间x(h)的函数关系式为y=mx+n,
把(0.5,75),(5,1125)代入得,$\left\{\begin{array}{l}{0.5m+n=75}\\{5m+n=1125}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{700}{3}}\\{n=-\frac{125}{3}}\end{array}\right.$
∴y=$\frac{700}{3}$x-$\frac{125}{3}$,
令y=0,则$\frac{700}{3}$x-$\frac{125}{3}$=0,解得x=$\frac{5}{28}$,
∴慢车比快车早出发$\frac{5}{28}$小时;
由图象直接可得出:快车追上慢车行驶了75千米,快车比慢车早2.5小时到达B地.
故答案为:$\frac{5}{28}$,75,2.5.
(2)∵OB=1125,
∴A、B两地之间的距离为1125千米;
则快车的速度为:$\frac{1125}{5-\frac{5}{28}}$=$\frac{700}{3}$(km/h).
慢车的速度=$\frac{1125}{7.5}$=150(km/h).
(3)当慢车还没有出发时:$\frac{20}{\frac{700}{3}}$=$\frac{3}{35}$(h);
当慢车出发后,快车还没有到达目的地时:$\frac{700}{3}$x-$\frac{125}{3}$-150x=20,解得:x=$\frac{37}{50}$;
当快车到达目的地后:5+$\frac{20}{150}$=$\frac{77}{15}$.
综上所述,当快车出发$\frac{3}{35}$h或$\frac{37}{50}$或$\frac{77}{15}$时,两车相距20km.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,正确由图象得出正确信息是解题关键,另外,解答(3)题时,要分类讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
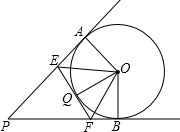 如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.
如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
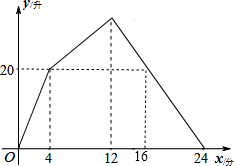 某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示
某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com