
【题目】单价为90元的商品经过两次降价后单价为60元,若每次降价的百分率都是x,则可列方程为_____.
科目:初中数学 来源: 题型:
【题目】阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH. 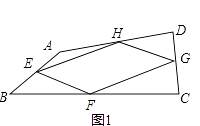
(1)这个中点四边形EFGH的形状是;
(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明. 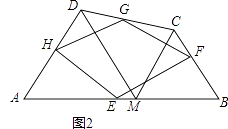
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
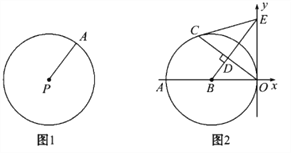
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
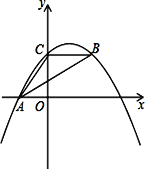
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列 ![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
⑴三角形的外角和是 ![]() ;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
A.( ![]() )(
)( ![]() )
)
B.( ![]() )(
)( ![]() )
)
C.( ![]() )(
)( ![]() )
)
D.( ![]() )(
)( ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com