
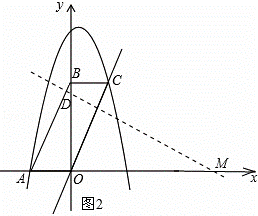
��ͼ��ƽ���ı���ABCD��ƽ��ֱ������ϵ�У���A������Ϊ����2��0������B������Ϊ��0��4����������y=��x2+mx+n������A��C��

��1���������ߵĽ���ʽ��
��2���������ߵĶԳ��Ὣƽ���ı���ABCO�ֳ������֣��Գ�����ಿ�ֵ�ͼ�������ΪS1���Ҳಿ��ͼ�ε������ΪS2����S1��S2�ıȣ�
��3����y����ȡһ��D�������ǣ�0��������ֱ��OC��x��ƽ�Ƶ�O��C�䣬��D����ֱ��O��C��ĶԳƵ��ΪD�䣬����D����������������ʱ�������ʱ��D�����겢ֱ��д��ֱ��O��C��ĺ�������ʽ��
�⣺��1����ͼ1��
���ı���ABCO��ƽ���ı��Σ�
��BC=OA��BC��OA��
��A����������2��0������B��������0��4����
���C��������2��4����
��������y=��x2+mx+n������A��C��
��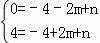 ��
��
��ã� ��
��
�������ߵĽ���ʽΪy=��x2+x+6��
��2����ͼ1��
�������ߵĽ���ʽΪy=��x2+x+6��
��Գ���x=�� =��
=��
��OC����ֱ�ߵĽ���ʽΪy=ax��
�ߵ�C������Ϊ��2��4����
��2a=4����a=2��
��OC����ֱ�ߵĽ���ʽΪy=2x��
��x=ʱ��y=1�����FΪ����1����
��S2=EC•EF
=����2��������4��1��=��
��S1=S�ı���ABCO��S2=2��4��= ��
��
��S1��S2= �� =23��9��
�� =23��9��
��S1��S2�ı�Ϊ23��9��
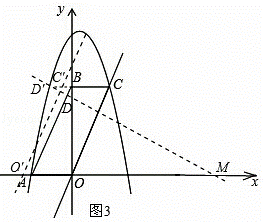
��3������D��DM��CO����x���ڵ�M����ͼ2��
�ߵ�C������Ϊ��2��4����
��tan��BOC=��
�ߡ�OMD=90�㩁��MOC=��BOC��
��tan��OMD=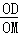 =��
=��
�ߵ�D�������ǣ�0������
�� =����OM=7��
=����OM=7��
���M��������7��0����
��ֱ��DM�Ľ���ʽΪy=kx+b��
����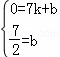 ��
��
��ã�
��ֱ��DM�Ľ���ʽΪy=��x+��
�ߵ�D���D�����ֱ��O��C��Գƣ�
��DD���O��C�䣬��DD����е���ֱ��O��C���ϣ�
��OC��O��C�䣬��DD���OC��
���D����ֱ��DM�������ߵĽ��㣮
����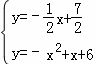
��ã�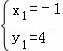 ��
�� ��
��
���D�����������1��4��������
��ֱ��O��C��Ľ���ʽΪy=2x+c��
�ٵ���D�������Ϊ����1��4��ʱ����ͼ3��
�߶�DD����е�Ϊ�� ��
�� ����������
����������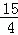 ����
����
����2��������+c=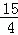 ��
��
��ã�c=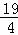 ��
��
��ʱֱ��O��C��Ľ���ʽΪy=2x+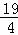 ��
��
�ڵ���D�������Ϊ������ʱ����ͼ4��
ͬ���ɵã���ʱֱ��O��C��Ľ���ʽΪy=2x+��
��������������D�������Ϊ����1��4��ʱ��ֱ��O��C��Ľ���ʽΪy=2x+ ������D�������Ϊ������ʱ��ֱ��O��C��Ľ���ʽΪy=2x+��
������D�������Ϊ������ʱ��ֱ��O��C��Ľ���ʽΪy=2x+��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ƽ��ֱ������ϵ�У�P�����ԭ��ĶԳƵ�ΪP1����3��������P�����x��ĶԳƵ�ΪP2��a��b������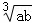 =��������
=��������
| �� | A�� | ��2 | B�� | 2 | C�� | 4 | D�� | ��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ҹ��Ŵ���ѧ�ҵó��ġ���ˬ��ͼ�������ĸ�ȫ�ȵ�ֱ�������κ�һ��С���������̹��ɵĴ������Σ���С��������������ε����֮��Ϊ1��13����ֱ�������ν϶̵�ֱ�DZ�a��ϳ���ֱ�DZ�b�ı�ֵΪ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
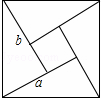
ij��ѧ�С������һ��������Ϸ�̣���ͼ��������Ϸ����Ͷ�����ڣ�Ͷ������Ӱ����ĸ����ǡ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ���ڡ�ABC�У���D��AB�ϣ���CD=CB����EΪBD���е㣬��FΪAC���е㣬����EF��CD�ڵ�M������AM��
��1����֤��EF=AC��
��2������BAC=45�㣬���߶�AM��DM��BC֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
| �� | A�� | ������Ľ�ˮ������80%����ʾ�������80%�ĵط����� |
| �� | B�� | Ϊ�˽�ѧ�������������ȡ��500��ѧ�����е��飬���е�������500��ѧ�� |
| �� | C�� | Ҫ�˽��������ξ��������������������ղ�ĵ��鷽ʽ |
| �� | D�� | һ������5��1��3��6��9����λ����5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��a��b��һ������30��ǵ�ֱ�����ǰ��������ͼ��ʾ��λ�ã�����1=24�㣬���2=���㡡��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�ǽ�����һ��·��ͳ�Ƶ�ij��ʱ�����������ij��٣���λ��ǧ��/ʱ�����������Щ���ij��ٵ���������λ���ֱ��ǣ�������
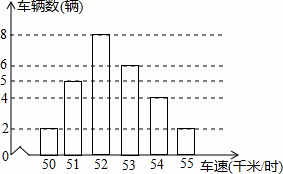
�� A�� 8��6 B�� 8��5 C�� 52��53 D�� 52��52
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������¼����ķ����������ҹ������ĸ߶����ӣ�Ѹ���ɳ��˽����ͷɻ�����غ��������Ѱ����ͼ����һ�ο�����Ѱ�У�ˮƽ���еķɻ��۲���ڵ�A����Ϊ30�㷽���F�㴦�����Ʒɻ��к������壨��������Ϊ��ֹ����Ϊ�˱��ڹ۲죬�ɻ�������ǰ������800����B�㣬��ʱ��õ�F�ڵ�B����Ϊ45��ķ����ϣ�������㵱�ɻ�����F������Ϸ���Cʱ����A��B��C��ͬһֱ���ϣ�����ֱ�߶�CFԼΪ�����ף�����������������ο���ֵ�� ��1.7��
��1.7��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com