
 如图,点E,F,G,H分别是菱形ABCD的四条边的中点,连接EF、FG、GH、HE,求证:四边形EFGH是矩形.
如图,点E,F,G,H分别是菱形ABCD的四条边的中点,连接EF、FG、GH、HE,求证:四边形EFGH是矩形. 分析 连接AC、BD,根据菱形的性质得到AC⊥BD,根据三角形中位线定理和平行四边形的判定定理证明四边形EFGH是平行四边形,根据三角形中位线定理证明EF⊥EH,得到答案.
解答 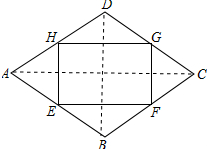 证明:连接AC、BD,如图所示:
证明:连接AC、BD,如图所示:
∵四边形ABCD是菱形,
∴AC⊥BD,
∵E、F分别是AB、BC上的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理,HG∥AC,HG=$\frac{1}{2}$AC,
则EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵F、G分别是BC、CD的中点,
∴HG∥BD,又∵EF∥AC,AC⊥BD,
∴EF⊥EH,
∴四边形EFGH是矩形.
点评 本题考查的是菱形的性质、矩形的判定、三角形中位线定理,掌握三角形中位线定理和矩形的判定定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
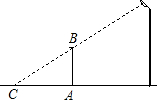 如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、B的坐标分别为(-1,-1),(-3,2).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、B的坐标分别为(-1,-1),(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com