
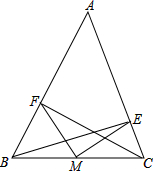
 如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.
如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
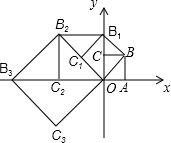 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com