
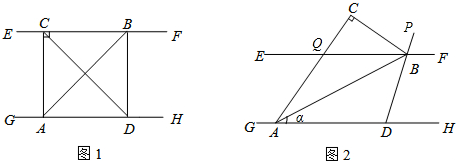
分析 (1)根据两直线平行,同旁内角互补求出∠CAD=90°,然后求出∠BAC=45°,从而得到∠ABC=45°,再根据BD平分∠FBC求出∠DBC=90°,然后求解即可;
(2)①EF∥GH,得出∠2=∠3,进一步得出∠1=∠3,利用三角形的内角和得出∠EBC,利用平角的意义得出∠PBC;
②根据两直线平行,内错角相等可得∠2=∠3,再根据三角形的内角和定理表示出∠4,然后表示∠5,再利用平角等于180°列式表示出∠DBA整理即可得解.
(3)根据(2)的结论计算即可得解.
解答 解:(1)∵EF∥GH,
∴∠CAD=180°-∠ACB=180°-90°=90°,
∵∠DAB=∠BAC,
∴∠BAC=45°,
∴∠ABC=45°,
∵BD平分∠FBC,
∴∠DBC=$\frac{1}{2}$×180°=90°,
∴∠DBA=90°-45°=45°;
(2)如图,
①∵EF∥GH,
∴∠2=∠3,
∵∠1=∠2=α,
∴∠1=∠3=α,
∵∠ACB=90°,
∴∠EBC=90°-∠1-∠3=90°-2α,
∠PBC=$\frac{1}{2}$(180°-∠EBC)=45°+α;
②设∠DAB=∠BAC=x,即∠1=∠2=x,
∵EF∥GH,
∴∠2=∠3,
在△ABC内,∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x,
∵直线BD平分∠FBC,
∴∠5=$\frac{1}{2}$(180°-∠4)=$\frac{1}{2}$(180°-180°+∠ACB+2x)=$\frac{1}{2}$∠ACB+x,
∴∠DBA=180°-∠3-∠4-∠5,
=180°-x-(180°-∠ACB-2x)-($\frac{1}{2}$∠ACB+x),
=180°-x-180°+∠ACB+2x-$\frac{1}{2}$∠ACB-x,
=$\frac{1}{2}$∠ACB,
=$\frac{1}{2}$×90°,
=45°;
(3)由(2)可知,
设∠DAB=∠BAC=x,即∠1=∠2=x,
∵EF∥GH,
∴∠2=∠3,
在△ABC内,∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x,
∵直线BD平分∠FBC,
∴∠5=$\frac{1}{2}$(180°-∠4)=$\frac{1}{2}$(180°-180°+∠ACB+2x)=$\frac{1}{2}$∠ACB+x,
∴∠DBA=180°-∠3-∠4-∠5,
=180°-x-(180°-∠ACB-2x)-($\frac{1}{2}$∠ACB+x),
=180°-x-180°+∠ACB+2x-$\frac{1}{2}$∠ACB-x,
=$\frac{1}{2}$∠ACB,
∠ACB=β时,
∠DBA=$\frac{1}{2}$β.
点评 本题考查了平行线的性质,角平分线的定义,三角形的内角和定理,熟记性质并理清图中各角度之间的关系是解题的关键.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中, A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.
(1)求点D的坐标
(2)四边形OCDB的面积
(3)在y轴上是否存在一点P,使 =
= ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).
某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
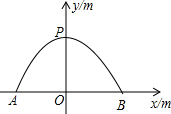 一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.
一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:填空题
已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为__________________

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 与计划相比 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com