

分析 (1)利用一等奖的人数÷对应的百分比求解即可;
(2)先求出二等奖的人数及优秀的人数,补全统计图即可;
(3)利用扇形统计图中优秀奖部分所对应的圆心角=360°×优秀奖的百分比求解即可;
(4)利用树状图,可知共有12种等可能的结果,其中恰好是1男1女的占8种,即可求出恰好是1男1女的概率.
解答 解:(1)全校参赛总获奖人数是4÷5%=80(人).
故答案为:80.
(2)二等奖的人数为:80×15%=12(人),
优秀的人数为:80-4-12-20=44(人),
补全统计图:
(3)扇形统计图中优秀奖部分所对应的圆心角是360°×$\frac{44}{80}$=198°.
故答案为:198.
(4)画树状图: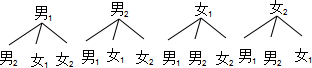
共有12种等可能的结果,其中恰好是1男1女的占8种,所以恰好是1男1女的概率为$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题主要考查了条形统计图及扇形统计图,解题的关键是能从条形统计图及扇形统计图得出相关数据.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M
已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M查看答案和解析>>
科目:初中数学 来源: 题型:解答题
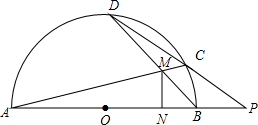 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3-\sqrt{5}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com