
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

【答案】(1)证明见解析;(2)四边形BEDF是菱形,理由见解析.
【解析】试题分析:(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中, 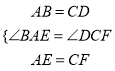 ,
,
∴△ABE≌△CDF(SAS);
(2)四边形BEDF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OB=OD,
∵DG=BG,
∴EF⊥BD,
∴四边形BEDF是菱形.


科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费,该市小明家今年9、10月份的用水量和所交水费如下表所示:
月份 | 用水量(m3) | 收费(元) |
9 | 5 | 7.5 |
10 | 9 | 18 |
设小明家每月用水量x(立方米),应交水费y(元).
⑴则a= ,b= ;
⑵ 当x≤6,x>6时,分别写出y与x的函数关系式;
⑶ 若该户11月份、12月份用水量为14立方米共交水费27元(11月份用水小于12月份用水),求该户11月份水、12月份用水各多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】-4,|-2|,-2,-(-3.5),0,-![]()
(1)在如图所示的数轴上表示出以上各数;
![]()
(2)比较以上各数的大小,用“<”号连接起来;
(3) 在以上各数中选择恰当的数填在下面这两个圈的重叠部分

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春节期间,在网络上用“百度”搜索引擎搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=-6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将ΔCEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
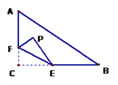
A. 1.6 B. 1.2 C. 1 D. 0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅去年开了一家商店,将每个月的盈亏情况都作了记录.今年1月份开始盈利,2月份盈利2000元,4月份盈利恰好2880元,若每月盈利的平均增长率都相同,这个平均增长率是( )
A. 20% B. 22% C. 25% D. 44%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com