练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
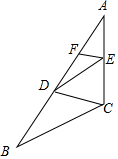
    16．如图，△ABC中，点D、F在边AB上，点E在边AC上，如果DE∥BC，EF∥CD，那么一定有（　　）
    A．DE2=AD•AEB．AD2=AF•ABC．AE2=AF•ADD．AD2=AE•AC

    分析 先证明△ADE∽△ABC得到AD：AB=AE：AC，再证明△AEF∽△ACD得到AF：AD=AE：AC，则AD：AB=AF：AD，然后利用比例的性质得到AD2=AF•AB．

    解答 解：∵DE∥BC，
    ∴△ADE∽△ABC，
    ∴AD：AB=AE：AC，
    ∵EF∥CD，
    ∴△AEF∽△ACD，
    ∴AF：AD=AE：AC，
    ∴AD：AB=AF：AD，
    ∴AD2=AF•AB．
    故选B．

    点评 本题考查了相似三角形的判定于性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在利用相似三角形的性质时利用相似比表示线段之间的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

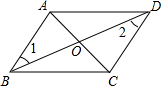    6．如图，在平行四边形ABCD中，对角线AC，BD交于点O，下列结论中错误的是（　　）
    A．∠1=∠2B．∠BAD=∠BCDC．AB=CDD．AO=BO

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各式由左边到右边的变形中，属于因式分解的是（　　）
    A．x2-2x+2=x（x-2）+2B．（x+y）（x-y）=x2-y2
    C．（2a-b）2=4a2-4ab+b2D．x2+4x+4=（x+2）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知∠A、∠B互余，∠A比∠B大30°，设∠A、∠B的度数分别为x°、y°，下列方程组中符合题意的是（　　）
    A．$\left\{\begin{array}{l}{x+y=180}\\{x=y-30}\end{array}\right.$B．$\left\{\begin{array}{l}{x+y=180}\\{x=y+30}\end{array}\right.$C．$\left\{\begin{array}{l}{x+y=90}\\{x=y-30}\end{array}\right.$D．$\left\{\begin{array}{l}{x+y=90}\\{x=y+30}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．下列说法错误的是（　　）
    A．1的平方根是±1B．-1的立方根是-1C．-3是$\sqrt{9}$的平方根D．$\sqrt{2}$是2的平方根

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图所示，能用一个字母表示的角有0个，以A为顶点的角有4个，图中所有角有15个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

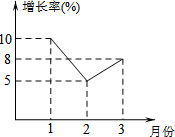    9．某市统计局统计了今年第一季度每月人均GDP的增长情况，并绘制了如图所示的统计图，下列结论：①1月份的人均GDP增长率最高；②2月份的人均GDP比1月份低；③这三个月的人均GDP都在增长，其中正确的结论序号是①③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，∠1=∠2，则下列结论一定成立的是（　　）
    A．∠B=∠DB．∠3=∠4C．∠D+∠BCD=180°D．∠D+∠BAD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．不等式组$\left\{\begin{array}{l}{1-x≥0}\\{2x-1＞-3}\end{array}\right.$的整数解是（　　）
    A．-1，0B．-1，1C．0，1D．-1，0，1

    查看答案和解析>>

    同步练习册答案