
【题目】现有甲骑电瓶车,乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园.设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图像如图①所示;甲、乙两人之间的路程差y关于x的函数图像如图②所示:
请你解决以下问题
(1)甲的速度是_____km/h;乙的速度是______km/h;
(2)对比图①、②可知:a=______;b=_____.
(3)乙出发多少时间,甲、乙两人路程差为7.5km?


【答案】(1)25;10;(2)10;![]() ;(3)乙出发
;(3)乙出发![]() 或
或![]() 小时,甲、乙两人路程差为7.5km .
小时,甲、乙两人路程差为7.5km .
【解析】
根据图像即可得出;
(2)结合图像,根据等量关系式解得得出;
(3)分时间段列二元一次方程即可得出.
有函数图像可知,
甲用了1h行驶了25km,根据v=![]() ,得v甲=
,得v甲=![]() =25km/h;
=25km/h;
乙用了2.5h行驶了25km,根据v=![]() ,得v乙=
,得v乙=![]() =10 km/h .
=10 km/h .
故答案分别为25,10.
b点:当甲、乙两人之间的路程差为0时,甲、乙两人相遇S乙=S甲
即25x-![]() =10x
=10x
解得:x=![]()
![]() b=
b=![]()
a:当x=1.5时,有图像可知,S甲=25km
将x=1.5代入S乙=10x中得
S乙=10![]() 1.5=15km
1.5=15km
乙之间路程差为:S甲-S乙=25-15=10km
故答案为:10;![]() ;
;
(3)由(2)可知:a=10,b=![]() ,
,
由(1)可知:当甲到达目的地时,甲的行驶时间为1h,乙的行驶时间为1.5h,此时a=10,
设y=mx+n(m≠0),
当![]() ≤ x≤1.5时,函数y=mx+n(m≠0)的图象经过(
≤ x≤1.5时,函数y=mx+n(m≠0)的图象经过(![]() ,0),(1.5,10)两点,
,0),(1.5,10)两点,
∴ ,解得
,解得![]()
∴y=15x-12.5, ![]() .
.
当1.5≤x≤2.5时,函数y=mx+n(m≠0)的图象经过(![]() ,0),(2.5,0)两点,
,0),(2.5,0)两点,
∴ ,解得
,解得![]() ,
,
∴y=-10x+25(1.5≤x≤2.5).
由题意得:15x-12.5=7.5或-10x+25=7.5,
解得:x=![]() ,或x=
,或x=![]() .
.
故乙出发![]() 或
或![]() 小时,甲、乙两人路程差为 7.5km .
小时,甲、乙两人路程差为 7.5km .


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
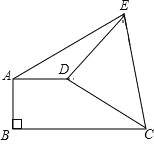
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长BC=8cm,宽AB=4cm的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长为( )

![]()

A. 4cmB. ![]() cmC.
cmC. ![]() cmD.
cmD. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使三角板的0cm刻度线与量角器的0°线在同一直线上,且直径DC是直角边BC的两倍,过点A作量角器圆弧所在圆的切线,切点为E,则点E在量角器上所对应的度数是____.
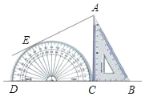
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半径为2的⊙O的直径,直线l与AB所在直线垂直,垂足为C,OC=3,P是圆上异于A、B的动点,直线AP、BP分别交l于M、N两点.
(1)当∠A=30°时,MN的长是 ;
(2)求证:MCCN是定值;
(3)MN是否存在最大或最小值,若存在,请写出相应的最值,若不存在,请说明理由;
(4)以MN为直径的一系列圆是否经过一个定点,若是,请确定该定点的位置,若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国为了实现到2020年达到全面小康社会的目标,近几年加大了扶贫工作的力度,合肥市某知名企业为了帮助某小型企业脱贫,投产一种书包,每个书包制造成本为18元,试销过程中发现,每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,据统计当售价定为30元/个时,每月销售40万个,当售价定为35元/个时,每月销售30万个.
(1)请求出k、b的值.
(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式.
(3)该小型企业在经营中,每月销售单价始终保持在25≤x≤36元之间,求该小型企业每月获得利润w(万元)的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com