
完成下列分析过程.
如图15所示,已知AB∥DC,AD∥BC,求证:AB=CD.
分析:要证AB=CD,只要证△________≌△________;需先证∠________=∠________,∠________=∠________.由已知“________∥________”,可推出∠________=∠________,________∥________,可推出∠________=∠________,且公共边________=________,因此,可以根据“________”判定△________≌△________.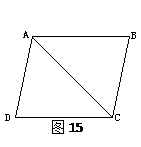
要证AB=CD,只要证△ABC≌△CDA;需先证∠BAC=∠DCA,∠ACB=∠CAD.
由已知“AB∥DC”,可推出∠BAC=∠DCA,AD∥BC,可推出∠ACB=∠CAD,且公共边AC=CA,因此,可以根据“角边角公理(ASA)”判定△ABC≌△CDA.
解析要证AB=CD,只要证明△ABC≌△CDA,已知AB∥DC,AD∥BC,所以有∠BAC=∠DCA,∠ACB=∠CAD,又因为AC是公共边,所以可根据ASA判定两三角形全等.
解:要证AB=CD,只要证△ABC≌△CDA;需先证∠BAC=∠DCA,∠ACB=∠CAD.由已知“AB∥DC”,可推出∠BAC=∠DCA,AD∥BC,可推出∠ACB=∠CAD,且公共边AC=CA,因此,可以根据“角边角(ASA)”判定△ABC≌△CDA.
故答案为:△ABC、△CDA、∠BAC、∠DCA、∠ACB、∠CAD、AB、DC、∠BAC、∠DCA、AD、BC、∠ACB、∠CAD、AC、CA、角边角(ASA)、△ABC、△CDA.


科目:初中数学 来源: 题型:
 10、完成下列分析过程.
10、完成下列分析过程.查看答案和解析>>
科目:初中数学 来源: 题型:
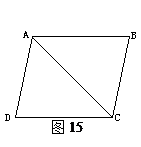
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
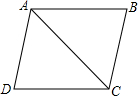 完成下列分析过程.
完成下列分析过程.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
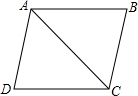
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com