
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.
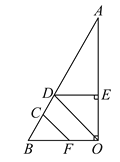
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
【答案】①垂直定义②同位角相等,两直线平行③两直线平行,内错角相等 ④已知⑤等量代换 ⑥同位角相等,两直线平行
【解析】由DE与BO都与AO垂直,利用垂直定义得到一对直角相等,利用同位角相等两直线平行得到DE与BO平行,利用两直线平行得到一对内错角相等,再由已知的一对角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得到CF与DO平行.
解:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°(垂直的定义)
∴DE∥BO(同位角相等两直线平行)
∴∠EDO=∠DOF(两直线平行内错角相等)
又∵∠CFB=∠EDO(已知)
∴∠DOF=∠CFB(等量代换)
∴CF∥DO(同位角相等两直线平行).
故答案为:垂直的定义;同位角相等两直线平行;两直线平行内错角相等;已知;等量代换;同位角相等两直线平行


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6 cm,BC=8 cm,沿对角线AC将矩形分成两个直角三角形,其中△ABC不动,△A′C′D沿射线CA的方向以每秒2 cm的速度移动.
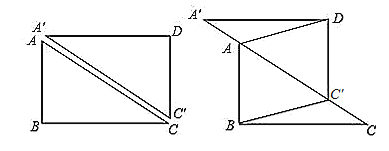
(1)在平移过程中,四边形ABC′D始终是 (请在下面的四个选项中选择一个你认为正确的序号填在横线上);
①平行四边形 ②矩形 ③菱形 ④正方形
(2)在移动过程中,当移动时间t(秒)为何值时,四边形ABC'D是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
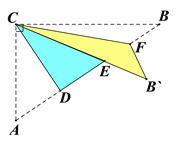
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积![]() =4.
=4.

(1)求直线AO的解析式;
(2)求反比例函数解析式;
(3)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
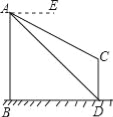
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件商品按成本价提高40%后标价,再打8折(标价的80%)销售,售价为240元,设这件商品的成本价为x元,根据题意,下面所列的方程正确的是( )
A. 40%x·80%=240
B. (1+40%)x·80%=240
C. 240×40%×80%=x
D. 40%x=240×80%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com