
分析 根据一个数的立方根等于它的算术平方根,可得x的值,根据立方根互为相反数的被开方数互为相反数,可得y的值,根据有理数的减法,可得答案.
解答 解:由$\sqrt{3x-2}$=$\root{3}{3x-2}$,得
3x-2=0或3x-2=1,
解得x=$\frac{2}{3}$或x=1.
由$\root{3}{x-3}$与$\root{3}{2-y}$互为相反数,得
x-3+2-y=0.
当x=$\frac{2}{3}$时,y=-$\frac{1}{3}$
当x=1时,y=0.
当x=$\frac{2}{3}$,y=-$\frac{1}{3}$时,x-y=$\frac{2}{3}$-(-$\frac{1}{3}$)=1;
当x=1,y=0时,x-y=1-0=1.
点评 本题考查了实数的性质,利用一个数的立方根等于它的算术平方根得出x的值,立方根互为相反数的被开方数互为相反数得出y的值是解题关键.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:选择题
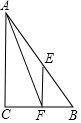 如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )
如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )| A. | △ABC是直角三角形 | B. | AF是△ABC的中位线 | ||
| C. | EF是△ABC的中位线 | D. | △BEF的周长为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
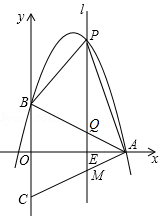 如图,在等腰△ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=ax2+$\frac{7}{2}$x+c经过A(8,0)、B(0,4)两点.
如图,在等腰△ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=ax2+$\frac{7}{2}$x+c经过A(8,0)、B(0,4)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
| 损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
| 苹果损坏的频率$\frac{m}{n}$(结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com