

分析 根据等边三角形的性质即可求出点P的坐标,进而即可得出部分点Pn的坐标,根据点的坐标的变化找出变化规律“P3n+1(3n+1,0),P3n+2(3n+1,0),P3n+3(3n+$\frac{5}{2}$,$\frac{\sqrt{3}}{2}$)(n为自然数)”,依此规律即可得出结论.
解答 解:∵△OAP为边长为1的正三角形,
∴点P的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
观察,发现:P1(1,0),P2(1,0),P3($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$),P4(4,0),P5(4,0),P6($\frac{11}{2}$,$\frac{\sqrt{3}}{2}$),P7(7,0),…,
∴P3n+1(3n+1,0),P3n+2(3n+1,0),P3n+3(3n+$\frac{5}{2}$,$\frac{\sqrt{3}}{2}$)(n为自然数).
∵2017=672×3+1,
∴点P2017的坐标为(2017,0).
故答案为:2017.
点评 本题考查了规律型中点的坐标以及等边三角形的性质,根据点的坐标的变化找出变化规律“P3n+1(3n+1,0),P3n+2(3n+1,0),P3n+3(3n+$\frac{5}{2}$,$\frac{\sqrt{3}}{2}$)(n为自然数)”是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
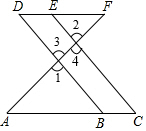 推理填空:
推理填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位;
如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE,BD,CE相交于点F,且∠ADB=∠DAE.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE,BD,CE相交于点F,且∠ADB=∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲岛争端持续,海监船加大对甲岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,甲岛位于O点,海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向甲岛所在地点O,海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船,求海监船行驶的航程BC的长.
甲岛争端持续,海监船加大对甲岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,甲岛位于O点,海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向甲岛所在地点O,海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船,求海监船行驶的航程BC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com