
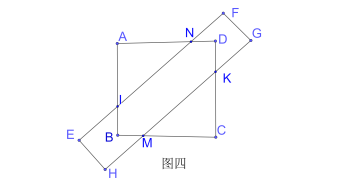
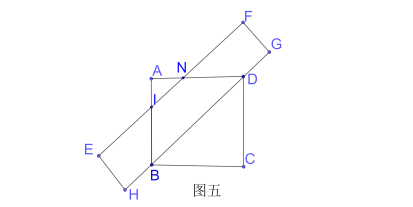
����Ŀ����ƽ���ϣ��߳�Ϊ![]() �������κͶ̱߳�Ϊ
�������κͶ̱߳�Ϊ![]() �ľ��μ��������غϣ���ͼ�٣��������κ;��ζ�ˮƽ����ʱ����������ص����
�ľ��μ��������غϣ���ͼ�٣��������κ;��ζ�ˮƽ����ʱ����������ص����![]() ��
��
�ס��ҡ�����λͬѧ�ֱ����������ͼ�β�ͬ���ص���ʽ��
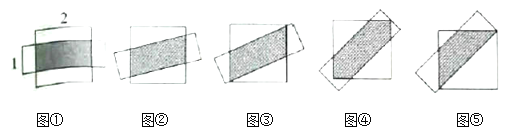
�ף��������ż���������ת����ͼ�ڵ�ͼ�۵Ĺ����У��ص����![]() ��С���䣮
��С���䣮
�ң���ͼ�ܣ��������ż������ļ�����ת�����ε����������������εĶԽ���ƽ��ʱ����ʱ���ص��������ͼ�۵��ص������
������ͼ�ݣ���ͼ���еľ��������Ϸ�ƽ�ƣ�ʹ���ε�һ������ǡ�þ��������εĶԽ��ߣ���ʱ���ص������![]() ��ͼ������С�ģ�
��ͼ������С�ģ�
����˵����ȷ���ǣ� ��
A.�ס��ҡ�������B.ֻ���Ҷ�C.ֻ�мײ���D.�ס��ҡ���������
���𰸡�C
��������
�����ص����������Ҫ���ͼ���ص㣬���öԳ����ʣ�ͨ������δ֪����ʾδ֪�߶Σ����������ʽ��⣬�������߶η�Χ�б������С��
��ͼһ��ʾ����AI=x��BJ=y������x+y=AB-IJ=2-1=1���ص������ı���JILK���Ϊ2��
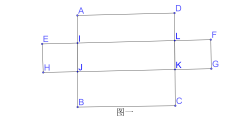
��ͼ����ʾ����AI=x��BJ=y��
��ΪJM=HE=1����JIMΪֱ�������Σ�б��JI����ֱ�DZ�JM��
���У�x+y��1���ص�����ƽ���ı���JILK���Ϊ![]() ��
��
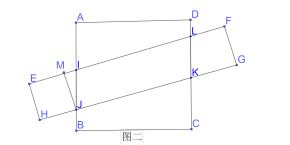
��ͼ����ʾ����AI=x��0��x��1����BJ=y=0���ص������ı���JIDK���Ϊ![]() ��
��
����ͼһ��ͼ����ת������У�x+y��ȡֵ��С�����ص�������������ʼ�ͬѧ˵������
��ͼ����ʾ����AI=AN=x��1��x��2�����ص����ֶ����BINDKM���Ϊ![]() ��
��
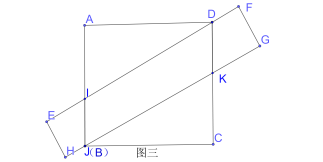
��0��x��2ʱ��![]() ������ͼ���ص����ֵ��������ͼ���ص������������ͬѧ˵����ȷ��
������ͼ���ص����ֵ��������ͼ���ص������������ͬѧ˵����ȷ��
��ͼ����ʾ����AI=AN=x�������ص������ı���INDB���Ϊ![]() ��
��
��Ϊ![]() �������ص��������С��2����С��ͼһ�ص������
�������ص��������С��2����С��ͼһ�ص������
���ϣ�ͼһ��ͼ���ص��������������ͼ�����С��ͼһ����ͼ�������С����ͬѧ˵����ȷ��
�ʴ�ΪCѡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
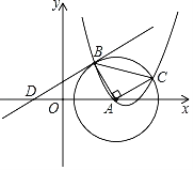
����Ŀ����ͼ����֪��Բ��Ϊ��![]() ��������y��ax2��
��������y��ax2��![]() x+c����A����
x+c����A����![]() ����B��C���㣬����AB��AC����AB��AC��B��C�����������ֱ���2��1��
����B��C���㣬����AB��AC����AB��AC��B��C�����������ֱ���2��1��
��1����B��C������������ߵĽ���ʽ��
��2��ֱ��y��kx+1������B����x�ύ�ڵ�D����E�����D���غϣ��ڸ�ֱ���ϣ���AD��AE�����жϵ�E�Ƿ��ڴ��������ϣ���˵�����ɣ�
��3�����ֱ��y��k1x��1���A���У���ֱ��д�������������ֱ�߽���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ˮ������Խ��Խ��ľ���ʼѡ�����þ�ˮ����һ�̼�ץס�̻����ӳ��ҹ�����A��B�����ͺż��þ�ˮ����160̨��A�ͺż��þ�ˮ��������150Ԫ/̨��B�ͺż��þ�ˮ��������350Ԫ/̨�����������ͺŵļ��þ�ˮ������ȥ36000Ԫ��
��1����A��B�����ͺż��þ�ˮ���������˶���̨��
��2��Ϊʹÿ̨B�ͺż��þ�ˮ����ë������A�ͺŵ�2�����ұ�֤������160̨���þ�ˮ����ë������11000Ԫ����ÿ̨A�ͺż��þ�ˮ�����ۼ������Ƕ���Ԫ����ע��ë����=�ۼ۩����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
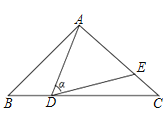
����Ŀ����ͼ������ABC�У�AB��AC��10����D�DZ�BC��һ���㣨����B��C�غϣ�����ADE����B������DE��AC�ڵ�E����cos������![]() �����н��ۣ�����ADE�ס�ACD���ڵ�BD��6ʱ����ABD����DCEȫ�ȣ�����DCEΪֱ��������ʱ��BDΪ8��
�����н��ۣ�����ADE�ס�ACD���ڵ�BD��6ʱ����ABD����DCEȫ�ȣ�����DCEΪֱ��������ʱ��BDΪ8��![]() ����0��CE��6.4��������ȷ�Ľ�����_________����������Ϊ��ȷ���۵���Ŷ����ϣ�
����0��CE��6.4��������ȷ�Ľ�����_________����������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ���ڡ�ABC�У���O��AC��һ�㣬����O��ֱ����AB��BC���ӳ��߷ֱ��ཻ�ڵ�M��N.
���������롿
(1)����O��AC���е㣬 ![]() ����
����![]() ��ֵ��
��ֵ��
��ܰ��ʾ������A��MN��ƽ���߽�BN���ӳ����ڵ�G.
��̽���о���
(2)����O��AC������һ��(����A��C�غ�)����֤�� ![]() ��
��
����չӦ�á�
(3)��ͼ����ʾ����P�ǡ�ABC������һ�㣬����AP��BP��CP�ֱ�BC��AC��AB�ڵ�D��E��F.��![]() ��
�� ![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǰ�Բ��ֱ����
�ǰ�Բ��ֱ����![]() Ϊ��Բ
Ϊ��Բ![]() ��Բ�ģ�
��Բ�ģ�![]() ���ң�ȡ
���ң�ȡ![]() ���е�
���е�![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
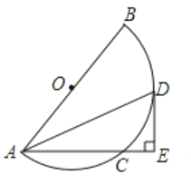
��1����֤��![]() �ǰ�Բ
�ǰ�Բ![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ʱ����
ʱ����![]() �ij���
�ij���
��3����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ������ʱ����
������ʱ����![]() ��ֱ��
��ֱ��![]() �ľ��룮
�ľ��룮
�鿴�𰸺ͽ���>>
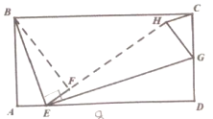
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��AD=8����EΪAD��һ�㣬����ABE��BE�۵��õ���FBE����GΪCD��һ�㣬����DEG��EG�۵��õ���HEG����E��F��H���㹲�ߣ�����CGHΪֱ��������ʱ��AE�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�D��BC���е㣬��G��AD�ϣ���G����A�غϣ�������G��ֱ�߽�AB��E��������AC�ڵ�F����AE=xAB��AF=yAC��x��y��0����
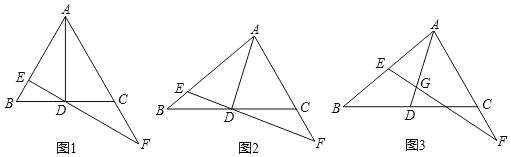
��1����ͼ1������ABCΪ�ȱ������Σ���G��D�غϣ���BDE=30����֤����AEF�ס�DEA��
��2����ͼ2������G��D�غϣ���֤��x+y=2xy��
��3����ͼ3����AG=nGD��x=![]() ��y=
��y=![]() ��ֱ��д��n��ֵ��
��ֱ��д��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��������ֻ��4���㣬��4��������һ�����ص����ʣ�����ÿ����ɵõ�6���߶Σ���6���߶�����ֻ�����ֳ��ȣ����ǰ����ĸ�������Ⱦ�㣮����������ABCD���ĸ�����(��ͼ1)����AB=BC=CD=DA��AC=BD����ʵ�����������ʵ�ͼ���кܶ࣬��ͼ2��A��B��C��O�ĸ��㣬����AB=BC=CA��OA=OB=OC����ͼ3��A��B��C��O�ĸ��㣬����OA=OB=OC=BC��AB=AC��
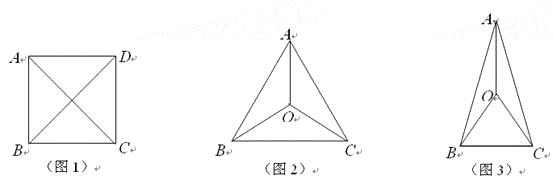
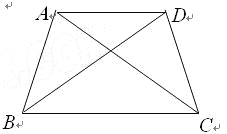
��1����ͼ������������ABCD���ĸ��������Ⱦ�㣬��AD��BC��
��д����ȵ��߶Σ�����������ĸ����
������BCD�Ķ�����
��2�����ٻ���һ���ı��Σ�ʹ�����ĸ�����Ϊ�Ⱦ�㣬��д����ȵ��߶Σ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com