
【题目】如图,抛物线的顶点为C(﹣1,﹣1),且经过点A、点B和坐标原点O,点B的横坐标为﹣3.
(1)求抛物线的解析式.
(2)求点B的坐标及△BOC的面积.
(3)若点D为抛物线上的一点,点E为对称轴上的一点,且以点A、O、D、E为顶点的四边形为平行四边形,请在左边的图上标出D和E的位置,再直接写出点D的坐标.

【答案】(1)y=(x+1)2﹣1 (2)(﹣3,3),3 (3)答案见解析
【解析】
(1)根据顶点坐标设出抛物线的顶点解析式,将原点坐标代入求出a的值,即可确定出抛物线的解析式.
(2)根据点B的横坐标,代入抛物线解析式求得点B坐标;过点B作BM⊥y轴于点M,过点C作CN⊥y轴于点N,构建一个直角梯形,进而求出△BOC的面积.
(3)根据题意分三种情况考虑,D在第一象限,第二象限以及第三象限,利用平行四边形的性质和坐标与图形的性质求出D的坐标即可.
解:(1)设抛物线解析式为y=a(x+1)2﹣1,
将点O(0,0)代入,得:a﹣1=0,
解得:a=1,
则抛物线解析式为y=(x+1)2﹣1;
(2)当x=﹣3时,y=3,
所以点B坐标为(﹣3,3),
如图1,过点B作BM⊥y轴于点M,过点C作CN⊥y轴于点N,
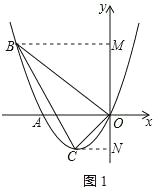
则BM=OM=3,CN=ON=1,
∴MN=4,
则S△BOC=S梯形BMNC﹣S△BOM﹣S△CON
=![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×3×3﹣
×3×3﹣![]() ×1×1
×1×1
=3;
(3)如图2所示,
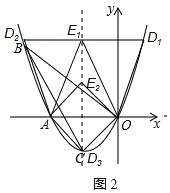
分三种情况考虑:
当D1在第一象限时,若四边形AOD1E1为平行四边形,
∴AO=E1D1=2,
∵抛物线对称轴为直线x=﹣1,
∴D1横坐标为1,
将x=1代入抛物线y=x2+2x=1+2=3,即D1(1,3);
当D2在第二象限时,同理D2(﹣3,3);
当D3在第三象限时,若四边形AE2OD3为平行四边形,此时D3与C重合,即D3(﹣1,﹣1);
综上,点D的坐标为(1,3)或(﹣3,3)或(﹣1,﹣1).


科目:初中数学 来源: 题型:
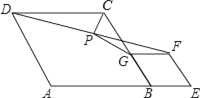
【题目】如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为了了解该区常驻市民对跑步、篮球、足球、羽毛球、舞蹈等体育项目的喜爱情况,在该区范围内随机抽取了若干名常驻市民,对他们喜爱以上的体育项目(每人只选一项)进行了问卷调查,将数据进行统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整)
(1)在这次问卷调查中,一共抽查 名常驻市民,篮球项目所占圆心角的度数是 ;估计该区1200万常驻市民中有 人喜爱足球运动、有 人喜欢跑步;
(2)补全频数分布直方图;
(3)若这次问卷调查中喜欢跑步的人员中有1名男士,喜欢舞蹈的人员中有2名女士,现从喜欢跑步和喜欢舞蹈的人员中随机选取两名作区代表参加重庆市的竞技比赛,用列表法或树状图求所选的两名恰好是一位喜欢跑步的男士和一位喜欢舞蹈的女士的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
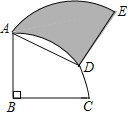
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ______
______
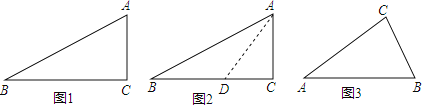
小天根据学习几何的经验,先画出了几何图形![]() 如图
如图![]() ,他发现
,他发现![]() 不是特殊角,但它是特殊角
不是特殊角,但它是特殊角![]() 的一半,若构造有特殊角的直角三角形,则可能解决这个问题
的一半,若构造有特殊角的直角三角形,则可能解决这个问题![]() 于是小天尝试着在CB边上截取
于是小天尝试着在CB边上截取![]() ,连接
,连接![]() 如图
如图![]() ,通过构造有特殊角
,通过构造有特殊角![]() 的直角三角形,经过推理和计算使问题得到解决.
的直角三角形,经过推理和计算使问题得到解决.
请回答:![]() ______.
______.
参考小天思考问题的方法,解决问题:
如图3,在等腰![]() 中,
中,![]() ,
,![]() ,请借助
,请借助![]() ,构造出
,构造出![]() 的角,并求出该角的正切值.
的角,并求出该角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于y轴对称,点
关于y轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于y轴,直线l的二次对称点.
是点P关于y轴,直线l的二次对称点.
![]() 如图1,点
如图1,点![]() .
.
![]() 若点B是点A关于y轴,直线
若点B是点A关于y轴,直线![]() :
:![]() 的二次对称点,则点B的坐标为______;
的二次对称点,则点B的坐标为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() :
:![]() 的二次对称点,则a的值为______;
的二次对称点,则a的值为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为______;
的表达式为______;
![]() 如图2,
如图2,![]() 的半径为
的半径为![]() 若
若![]() 上存在点M,使得点
上存在点M,使得点![]() 是点M关于y轴,直线
是点M关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,b的取值范围是______;
上,b的取值范围是______;
![]() 是x轴上的动点,
是x轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点N,使得点
上存在点N,使得点![]() 是点N关于y轴,直线
是点N关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在y轴上,求t的取值范围.
在y轴上,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当﹣![]() <x<2时,y<0;
<x<2时,y<0;
(3)a﹣b+c=0;
(4)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧
则其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
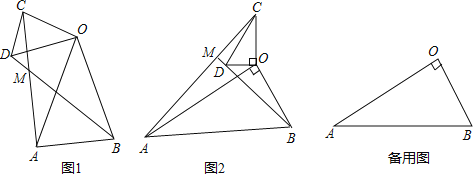
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com