
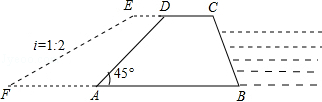

 EG。∴四边形EGHD是矩形。
EG。∴四边形EGHD是矩形。 ,∴FG=2EG=16(米),
,∴FG=2EG=16(米), ×(2+10)×8×400=19200(立方米).
×(2+10)×8×400=19200(立方米).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
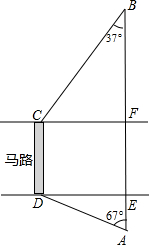
 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
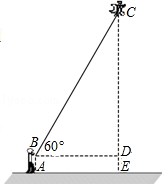
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 +1,AD=
+1,AD= .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ;②cosB=
;②cosB= ;③tanA=
;③tanA= ;④tanB=
;④tanB= ,其中正确的结论是 (只需填上正确结论的序号)
,其中正确的结论是 (只需填上正确结论的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com