
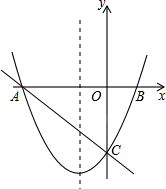
 如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.
如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.分析 (1)首先求得m的值求得一次函数,进一步求得C点坐标,根据二次函数对称性求得点B点坐标,利用交点式求得抛物线的解析式;
(2)确定对称轴上是否存在一点P,使得△PBC的周长最小,利用轴对称的性质和两点之间线段最短的原理解决;
(3)把△PDE的面积为S看成S△AOC-S△DOE-S△PDC-S△PEA,设出CD长度,表示出各个三角形的底和高,利用面积建立二次函数求得最值即可.
解答 解:(1)∵y=-$\frac{2}{3}$x+m经过点A(-3,0),
∴0=2+m,解得m=-2,
∴直线AC解析式为y=-$\frac{2}{3}$x-2,
∴C(0,-2).
∵抛物线y=ax2+bx+c对称轴为x=-1,且与x轴交于A(-3,0),
∴另一交点为B(1,0),设抛物线解析式为y=a(x+3)(x-1),
∵抛物线经过 C(0,-2),∴-2=a•3×(-1),解得a=$\frac{2}{3}$,
∴抛物线解析式为y=$\frac{2}{3}$x2+$\frac{4}{3}$x-2;
(2)要使△PBC的周长最小,只需BP+CP最小即可.如图1,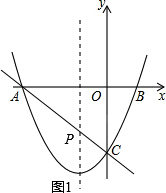
连接AC交x=-1于P点,因为点A、B关于x=-1对称,根据轴对称性质以及两点之间线段最短,可知此时BP+CP最小(BP+CP最小值为线段AC的长度).
∵A(-3,0),B(1,0),C(0,-2),
∴直线AC解析式为y=-$\frac{2}{3}$x-2,
∵xP=-1,∴yP=-$\frac{4}{3}$,即P(-1,-$\frac{4}{3}$).
(3)如图2,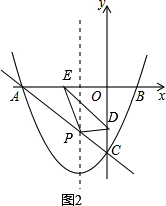
∵设CD的长为m,△PDE的面积为S
∴D(0,m-2),
∵DE‖PC,直线AC解析式为y=-$\frac{2}{3}$x-2,
∴设直线DE解析式:y=-$\frac{2}{3}$x+m-2,
当y=0时,x=$\frac{3}{2}$m-3,
∴E($\frac{3}{2}$m-3,0)
S△PDE=S△AOC-S△DOE-S△PDC-S△PEA
=3-$\frac{1}{2}$×$\frac{3}{2}$m×$\frac{4}{3}$-$\frac{1}{2}$×(3-$\frac{3}{2}$m)×(2-m)-$\frac{1}{2}$×m×1
=-$\frac{3}{4}$m2+$\frac{3}{2}$m
=-$\frac{3}{4}$(m-1)2+$\frac{3}{4}$
∴当m=1时有最大值$\frac{3}{4}$.
点评 此题考查二次函数综合题,考查待定系数法求函数解析式,二次函数的对称性,两点间的距离公式、轴对称-最短路线问题等,运算比较复杂,注意解题的灵活性与综合能力的提高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 年数n | 高度h(厘米) |
| 第1年 | 100 |
| 第2年 | 100+5 |
| 第3年 | 100+10 |
| 第4年 | 100+15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com