
【题目】教材的![]() 课题学习
课题学习![]() 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
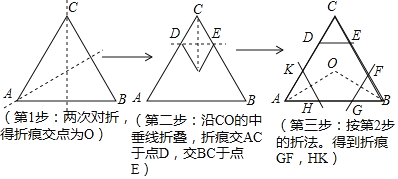
请你根据小明同学的折叠方法,回答以下问题: ![]() 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么![]() ______
______ ![]() 用含a的式子表示
用含a的式子表示![]() ;
;
![]() 根据折叠性质可以知道
根据折叠性质可以知道![]() 的形状为______ 三角形;
的形状为______ 三角形;
![]() 请同学们利用
请同学们利用![]() 、
、![]() 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
【答案】 ![]() 等边
等边
【解析】试题分析:(1)根据折叠的性质即可得到结论;
(2)根据折叠的性质即可得到结论;
(3)由(2)知△CDE为等边三角形,根据等边三角形的性质得到CD=CE=DE=![]() CO÷cos30°=
CO÷cos30°=![]() a,求得∠ADE=∠BED=120°,同理可得,AH=AK=KH=
a,求得∠ADE=∠BED=120°,同理可得,AH=AK=KH=![]() a,BG=BF=GF=
a,BG=BF=GF=![]() a,∠CKH=∠BHK=120°,由于AB=BC=AC=a,于是得到结论.
a,∠CKH=∠BHK=120°,由于AB=BC=AC=a,于是得到结论.
试题解析:(1)∵正三角形ABC的边长为a,
由折叠的性质可知,点O是三角形的重心,
∴CO=![]() a;
a;
故答案为: ![]() a;
a;
(2)△CDE为等边三角形;
故答案为:等边;
(3)由(2)知△CDE为等边三角形,
∴CD=CE=DE=![]() CO÷cos30°=
CO÷cos30°=![]() a,
a,
∠ADE=∠BED=120°,
同理可得,AH=AK=KH=![]() a,BG=BF=GF=
a,BG=BF=GF=![]() a,∠CKH=∠BHK=120°,
a,∠CKH=∠BHK=120°,
∵AB=BC=AC=a,
∴DE=DK=KH=HG=GF=FE=![]() a,∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
a,∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
∴六边形KHGFED是一个正六边形.


科目:初中数学 来源: 题型:
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果![]() ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )

A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).[图(2)为解答备用图]
).[图(2)为解答备用图]
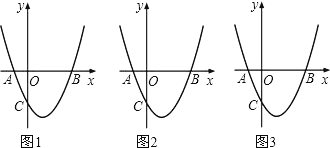
(1)![]() __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)
(1)如图1,在ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F.求证:△AOE≌△COF;

(探究)
(2)如图2,在菱形ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F,若AC=4,BD=8,求四边形ABFE的面积.
(应用)
(3)如图3,边长都为1的5个正方形如图摆放,试利用无刻度的直尺,画一条直线平分这5个正方形组成的图形的面积.(要求:保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b满足![]() .请回管问题:
.请回管问题:
(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,![]() 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.
(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
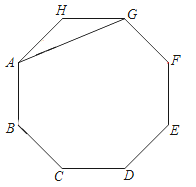
【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )

A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com