练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】王刚同学拟了一张招领启事：“今天拾到钱包一个，内有人民币8.5元，请失主到一（1）班认领”．你认为这个启事合理吗？如果不合理，问题在哪里？请你改正过来．

    【答案】解：不合格，问题出在8.5元上，应该写为n元．
    【解析】根据应用文的要求，应该把8.5改为字母．
    【考点精析】本题主要考查了用字母表示数的相关知识点，需要掌握单独一个数或者一个字母也是代数式才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

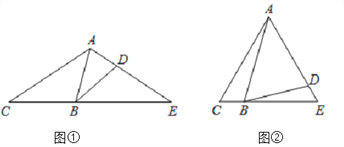
    【题目】探究：如图①，△ACE中，AC=AE，点B在边CE上，点D在边AE上，∠ABD=∠E．求证：△ACB∽△BED．

    应用：如图②，△ACE为等边三角形，点B在边CE上，点D在边AE上，∠ABD=60°，BC=BE，则△ABD与△BDE的面积比为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解全校学生的上学方式，在全校1000名学生中随机抽取了150名学生进行调查．下列说法正确的是（　　）

    A. 总体是全校学生

    B. 样本容量是1000

    C. 个体是每名学生的上学时间

    D. 样本是随机抽取的150名学生的上学方式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

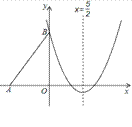
    【题目】如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线经过点B，且顶点在直线上.

    （1）求抛物线对应的函数关系式；

    （2）若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图所示，B、C、D三点在同一条直线上，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（　　）

    A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】体育委员带了500元钱去买体育用品，已知一个足球a元，一个篮球b元，说明代数式500﹣3a﹣2b表示的意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若（a+b）2＝5，（a﹣b）2＝3，则a2+b2＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：（1）6x-7x+1=0；（2）4x-3x=52；

    （3）（x-2）（x-3）=12；（4）5x-18=9x

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图点D、E分别在等边ΔABC边BC、CA上，且CD=AE,联结AD、 BE.

    (1)求证：BE=AD；

    (2)延长DA交BE于F,求∠BFD的度数.

    查看答案和解析>>

    同步练习册答案