
【题目】如图,AB 为圆O的直径, PQ切圆O于T , AC⊥PQ于C ,交圆O于 D .

(1)求证: AT 平分∠BAC ;
(2)若 AD =2 , TC=![]() ,求圆O的半径.
,求圆O的半径.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)PQ切⊙O于T,则OT⊥PC,根据AC⊥PQ,则AC∥OT,要证明AT平分∠BAC,只要证明∠TAC=∠ATO就可以了.
(2)过点O作OM⊥AC于M,则满足垂径定理,在直角△AOM中根据勾股定理就可以求出半径OA.
试题解析:(1)连接OT;

∵PQ切⊙O于T,
∴OT⊥PQ,
又∵AC⊥PQ,
∴OT∥AC,
∴∠TAC=∠ATO;
又∵OT=OA,
∴∠ATO=∠OAT,
∴∠OAT=∠TAC,
即AT平分∠BAC.
(2)过点O作OM⊥AC于M,
∴AM=MD=![]() =1;
=1;
又∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,
∴OM=TC=![]() ,
,
∴在Rt△AOM中,
AO=![]() =
=![]() =2;
=2;
即⊙O的半径为2.


科目:初中数学 来源: 题型:
【题目】书籍是人类进步的阶梯,联合国教科文组织把每年的4月23日确定为“世界读书日”,某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数 | 43 | 31 | 15 | 5 | 4 | 2 |
请你根据以上信息解答下列问题:
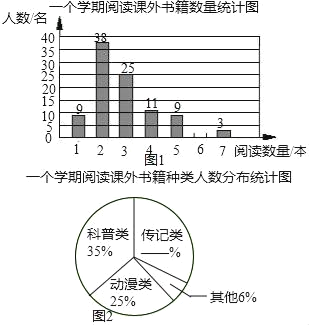
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有1200名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的两直角边
的两直角边![]() ,
,![]() 分别在
分别在![]() 轴的负半轴和
轴的负半轴和![]() 轴的正半轴上,
轴的正半轴上,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且顶点在直线
,且顶点在直线![]() 上.
上.

(1)求抛物线对应的函数关系式;
(2)若![]() 是由
是由![]() 沿
沿![]() 轴向右平移得到的,当四边形
轴向右平移得到的,当四边形![]() 是菱形时,试判断点
是菱形时,试判断点![]() 和点
和点![]() 是否在该抛物线上,并说明理由;
是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若![]() 点是
点是![]() 所在直线下方抛物线上的一个动点,过点
所在直线下方抛物线上的一个动点,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长度为
的长度为![]() .求
.求![]() 与
与![]() 之间的函数关系式,写出自变量
之间的函数关系式,写出自变量![]() 的取值范围,并求
的取值范围,并求![]() 取最大值时,点
取最大值时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:若点![]() 在某一个函数的图象上,且点
在某一个函数的图象上,且点![]() 的横纵坐标相等,我们称点
的横纵坐标相等,我们称点![]() 为这个函数的“好点”.若关于
为这个函数的“好点”.若关于![]() 的二次函数
的二次函数![]() 对于任意的常数
对于任意的常数![]() 恒有两个“好点”,则
恒有两个“好点”,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如图1,当![]() 时.
时.
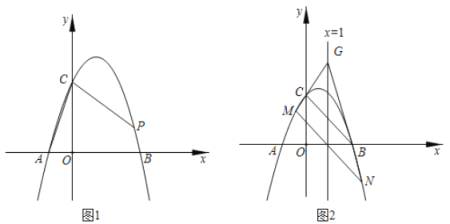
①直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②若抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)如图2,平移直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 在定直线
在定直线![]() 上运动,求
上运动,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() 为常数,
为常数,![]() )的图像与
)的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() ,半径为4的⊙
,半径为4的⊙![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在点
在点![]() 上方.
上方.

(1)若直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() .
.
①求![]() 的度数;
的度数;
②用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)设![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com