
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,点
,点![]() 、
、![]() 在⊙
在⊙![]() 上,
上,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() ,
,![]() ,有以下结论:①
,有以下结论:①![]() ;②劣弧
;②劣弧![]() 的长为
的长为![]() ;③点
;③点![]() 为
为![]() 的中点;④
的中点;④![]() 平分
平分![]() ,以上结论一定正确的是______.
,以上结论一定正确的是______.
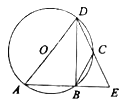
【答案】①②③
【解析】
①根据圆内接四边形的外角等于其内对角可得∠CBE=∠ADE,根据等边对等角得出∠CBE=∠E,等量代换即可得到∠ADE=∠E;
②根据圆内接四边形的外角等于其内对角可得∠A=∠BCE=70![]() ,根据等边对等角以及三角形内角和定理求出∠AOB=40
,根据等边对等角以及三角形内角和定理求出∠AOB=40![]() ,再根据弧长公式计算得出劣弧
,再根据弧长公式计算得出劣弧![]() 的长;
的长;
③根据圆周角定理得出∠ACD=90![]() ,即AC⊥DE,根据等角对等边得出AD=AE,根据等腰三角形三线合一的性质得出∠DAC=∠EAC,再根据圆周角定理得到点C为
,即AC⊥DE,根据等角对等边得出AD=AE,根据等腰三角形三线合一的性质得出∠DAC=∠EAC,再根据圆周角定理得到点C为![]() 的中点;
的中点;
④由DB⊥AE,而∠A≠∠E,得出BD不平分∠ADE.
①∵ABCD是⊙O的内接四边形,
∴∠CBE=∠ADE,
∵CB=CE,
∴∠CBE=∠E,
∴∠ADE=∠E,故①正确;
②∵∠A=∠BCE=70![]() ,
,
∴∠AOB=40![]() ,
,
∴劣弧![]() 的长=
的长=![]()
![]() ,故②正确;
,故②正确;
③∵AD是⊙O的直径,
∴∠ACD=90![]() ,即AC⊥DE,
,即AC⊥DE,
∵∠ADE=∠E,
∴AD=AE,
∴∠DAC=∠EAC,
∴点C为![]() 的中点,故③正确;
的中点,故③正确;
④∵DB⊥AE,而∠A≠∠E,
∴BD不平分∠ADE,故④错误.
所以正确结论是①②③.
故答案为①②③.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:
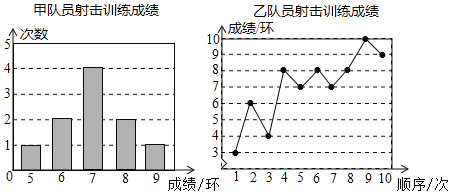
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)a=_____;b=_____;c=_____;
(2)填空:(填“甲”或“乙”).
①从平均数和中位数的角度来比较,成绩较好的是_____;
②从平均数和众数的角度来比较,成绩较好的是_____;
③成绩相对较稳定的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
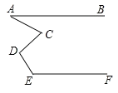
A. ∠A+∠C+∠D+∠E=360°B. ∠A-∠C+∠D+∠E=180°
C. ∠E-∠C+∠D-∠A=90°D. ∠A+∠D=∠C+∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B两小区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
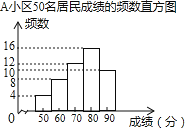
(信息一)A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求A小区50名居民成绩的中位数.
(2)请估计A小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析A,B两小区居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
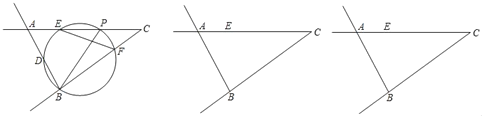
【题目】如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F.
(1)当点P在线段AC上时,若点E为![]() 中点,求BP的长.
中点,求BP的长.
(2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值.
(3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则![]() 的值为 .(直接写出答案即可)
的值为 .(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
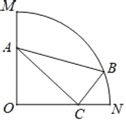
【题目】如图,在扇形OMN中,∠MON=90°,OM=6,△ABC是扇形的内接三角形,其中A、C、B分别在半径OM、ON和弧MN上,∠ACB=90°,BC:AC=3:8,则线段BC的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com