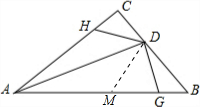
证明:(1)在AB上取一点M,使得AM=AH,连接DM,
∵
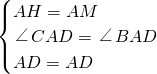
,
∴△AHD≌△AMD,
∴HD=MD,∠AHD=∠AMD,
∵HD=DB,
∴DB=MD,
∴∠DMB=∠B,
∵∠AMD+∠DMB=180°,
∴∠AHD+∠B=180°,
即∠B与∠AHD互补.
(2)由(1)∠AHD=∠AMD,HD=MD,∠AHD+∠B=180°,
∵∠B+2∠DGA=180°,∠AHD=2∠DGA,
∴∠AMD=2∠DGM,
又∵∠AMD=∠DGM+∠GDM,
∴2∠DGM=∠DGM+∠GDM,即∠DGM=∠GDM,
∴MD=MG,
∴HD=MG,
∵AG=AM+MG,
∴AG=AH+HD.
分析:(1)在AB上取一点M,使得AM=AH,连接DM,则利用SAS可得出△AHD≌△AMD,从而得出HD=MD=DB,即有∠DMB=∠B,通过这样的转化可证明∠B与∠AHD互补.
(2)由(1)的结论中得出的∠AHD=∠AMD,结合三角形的外角可得出∠DGM=∠GDM,可将HD转化为MG,从而在线段AG上可解决问题.
点评:本题考查了全等三角形的判定及性质,结合了等腰三角形的知识,解决这两问的关键都是通过全等图形的对应边相等、对应角相等,将题目涉及的角或边进行转化.

 如图,AD是△ABC的角平分线,H,G分别在AC,AB上,且HD=BD.
如图,AD是△ABC的角平分线,H,G分别在AC,AB上,且HD=BD. 证明:(1)在AB上取一点M,使得AM=AH,连接DM,
证明:(1)在AB上取一点M,使得AM=AH,连接DM,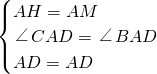 ,
,

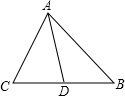 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.