
����Ŀ��ijˮ�������̵�������ֲ���زɹ����ѣ�������һ���Բɹ����ѵIJɹ�����y��Ԫ/ǧ�ˣ���ɹ���x��ǧ�ˣ�֮��ĺ�����ϵͼ����ͼ������AB��BC��CD��ʾ���������˵�A����
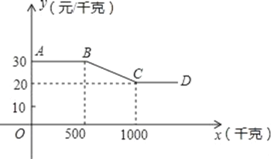
��1����500��x��1000ʱ��д��y��x֮��ĺ�����ϵʽ��
��2�����ѵ���ֲ�ɱ�Ϊ8Ԫ/ǧ�ˣ�ij������һ���Բɹ����ѵIJɹ���������1000ǧ�ˣ����ɹ����Ƕ���ʱ��������ֲ���ػ��������������Ƕ���Ԫ��
��3���ڣ�2���������£���������һ���Ը���16800Ԫ����������ֲ���ؿ��Ի�ö���Ԫ������
���𰸡���1��y��x֮��ĺ�����ϵʽΪ��y����0.02x+40��
��2��һ���Բɹ���Ϊ800ǧ��ʱ���߲���ֲ�����ܻ���������Ϊ12800Ԫ��
��3����������һ���Ը���16800Ԫ���������ֲ���ؿ��Ի��12000Ԫ������
��������
��1���ȵó���![]() ��ͼ���ϣ������ô���ϵ������⼴�ɣ�
��ͼ���ϣ������ô���ϵ������⼴�ɣ�
��2����![]() ��
��![]() ����������ֱ�ó����������ٸ���һ�κ����Ͷ��κ�������������⼴�ɣ�
����������ֱ�ó����������ٸ���һ�κ����Ͷ��κ�������������⼴�ɣ�
��3���ȸ��ݾ����̸��Ļ���������ɹ���Ϊ![]() ���ٸ����⣨1���Ľ��ۺͻ����һ��һԪ���η��̣�����ɹ���x��ֵ���ٴ����⣨2�������������ɵã�
���ٸ����⣨1���Ľ��ۺͻ����һ��һԪ���η��̣�����ɹ���x��ֵ���ٴ����⣨2�������������ɵã�
��1���赱![]() ʱ��y��x֮��ĺ�����ϵʽΪ
ʱ��y��x֮��ĺ�����ϵʽΪ![]()
�����⣬����![]() �����
�����![]()
���![]()
�ʵ�![]() ʱ��y��x֮��ĺ�����ϵʽΪ
ʱ��y��x֮��ĺ�����ϵʽΪ![]() ��
��
��2�����ɹ�����xǧ��ʱ���߲���ֲ���ػ���WԪ
��![]() ʱ��
ʱ��![]()
��һ�κ����������Եã�W��x�����������
��![]() ʱ��Wȡ�����ֵ�����ֵΪ
ʱ��Wȡ�����ֵ�����ֵΪ![]() Ԫ
Ԫ
��![]() ʱ��
ʱ��![]()
���⣨1���ã�![]()
�����ã�![]()
�ɶ��κ����������Եã���![]() ʱ��W��x�����������
ʱ��W��x�����������![]() ʱ��W��x���������С
ʱ��W��x���������С
��![]() ʱ��Wȡ�����ֵ�����ֵΪ12800Ԫ
ʱ��Wȡ�����ֵ�����ֵΪ12800Ԫ
���ϣ�һ���Բɹ���Ϊ800ǧ��ʱ���߲���ֲ���ػ�������������Ϊ12800Ԫ��
��3����![]() ʱ��
ʱ��![]() ���ɹ��ܷ���Ϊ
���ɹ��ܷ���Ϊ![]() Ԫ
Ԫ
��![]() ʱ��
ʱ��![]() ���ɹ��ܷ���Ϊ
���ɹ��ܷ���Ϊ![]() Ԫ
Ԫ
![]()
��þ�����һ���Բɹ���![]()
�ɣ�1��֪����ʱ�þ����̲ɹ�����Ϊ![]()
������ã�![]()
���![]() �����������⣬��ȥ����
�����������⣬��ȥ����![]()
��![]() ʱ��������ֲ���ؿɻ������Ϊ
ʱ��������ֲ���ؿɻ������Ϊ![]() ��Ԫ����
��Ԫ����
����������һ���Ը���16800Ԫ���������ֲ���ؿ��Ի��12000Ԫ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+c����A��0����4����B��2��0�����㣮
��1����c��ֵ��a��b����Ĺ�ϵʽ��
��2������������A��B����䣬��������������a��ȡֵ��Χ��
��3��������ͬʱ����������ͬ�ĵ�M��p��m����N����2��p��n����
����m��n����a��ֵ��
����m����2p��3��n��2p+1����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�AD��y�ᣬ����Ϊ��E������A�ڵڶ����ޣ�����B��y����������ϣ�����������y=![]() ��k��0��x��0����ͼ��ͬʱ��������C��D������C�ĺ�����Ϊ5��BE=3DE����k��ֵΪ��������
��k��0��x��0����ͼ��ͬʱ��������C��D������C�ĺ�����Ϊ5��BE=3DE����k��ֵΪ��������

A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʵ�����е�һ�ְڶ�װ�ã�![]() �ڵ����ϣ�֧��
�ڵ����ϣ�֧��![]() �ǵױ�Ϊ
�ǵױ�Ϊ![]() �ĵ���ֱ�������Σ��ڶ��۳�
�ĵ���ֱ�������Σ��ڶ��۳�![]() ���Ƶ�
���Ƶ�![]() ��ת���ڶ���
��ת���ڶ���![]() ���Ƶ�
���Ƶ�![]() ��ת��
��ת��![]() ��
��![]() .
.

��1������ת�����У�
�ٵ�![]() ������ͬһֱ����ʱ����
������ͬһֱ����ʱ����![]() �ij���
�ij���
�ڵ�![]() ������ͬһֱ�������εĶ���ʱ����
������ͬһֱ�������εĶ���ʱ����![]() �ij�.
�ij�.
��2�����ڶ���![]() ˳ʱ����ת
˳ʱ����ת![]() ����
����![]() �����
��λ����![]() ��ĵ�
��ĵ�![]() ת�����ڵĵ�
ת�����ڵĵ�![]() ��������
��������![]() ����ͼ2����ʱ
����ͼ2����ʱ![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��x+4��ͼ���뷴��������y��![]() ��kΪ������k��0����ͼ����A����1��3����B��b��1�����㣮
��kΪ������k��0����ͼ����A����1��3����B��b��1�����㣮
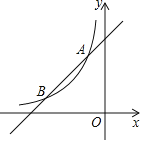
��1�����������ı���ʽ��
��2����x������һ��P��ʹPA+PB��ֵ��С���������������ĵ�P�����ꣻ
��3������OA��OB�����OAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������y=![]() ��ͼ�������A��2��3����B����3��n�����㣮
��ͼ�������A��2��3����B����3��n�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
��3������B��BC��x�ᣬ����ΪC����S��ABC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ö��ƱͼƬ��״��ȫ��ͬ���ֱ����ҹ�����ѧ�����֮����ʱ�䡢�ź⡢ɮһ�У�������ͼƬ�����һ��

��1���������ȡһ��ͼƬ�������������֮��ͼƬ�ĸ�����__________��
��2���������ȡһ��ͼƬȻ��Żأ��������ȡһ��ͼƬ�������б�����״ͼ������������һ�����������֮��ͼƬ�ĸ��ʣ�
��3��С����С����С�ϡ�С����λͬѧ������ȡͼƬ����С�����������֮��ͼƬ����ʣ��������(��������)
A��С����������ʱ�䡱ͼƬ�ĸ��ʴ�����B��С����������ʱ�䡱ͼƬ�ĸ��ʴ�
C��С����������ʱ�䡱ͼƬ�ĸ��ʴ�����D��������������ʱ�䡱ͼƬ�ĸ���һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������y=![]() ��ͼ�������A��2��3����B����3��n�����㣮
��ͼ�������A��2��3����B����3��n�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
��3������B��BC��x�ᣬ����ΪC����S��ABC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
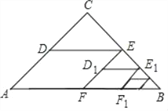
����Ŀ����ͼ,��ABC��,��C=90��,AC=BC=2,ȡBC���е�E,��ED��AB,EF��AC,�õ��ı���EDAF,�����������S1��ȡBE�е�E1����E1D1��FB��E1F1��EF,�õ��ı���E1D1FF1�������������S2���մ˹�������ȥ,��S1=_______��S2017=____________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com