
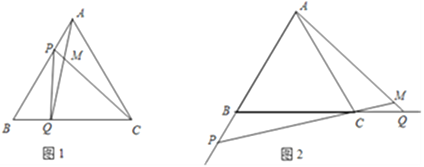
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

【答案】见解析
【解析】试题分析:(1)因为点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,所以AP=BQ.AB=AC,∠B=∠CAP=60°,因而运用边角边定理可知△ABQ≌△CAP.再用全等三角形的性质定理及三角形的角间关系、三角形的外角定理,可求得CQM的度数;
(2)设时间为t,则AP=BQ=t,PB=4-t.分别就①当∠PQB=90°时;②当∠BPQ=90°时利用直角三角形的性质定理求得t的值;
(3)首先利用边角边定理证得△PBC≌△QCA,再利用全等三角形的性质定理得到∠BPC=∠MQC.再运用三角形角间的关系求得∠CMQ的度数.
试题解析:(1)∠CMQ不变.
AC="BA," ∠A=∠B, AP="BQ,"
∴△ACP≌△BAQ, ∴∠ACP=∠BAQ,
∴∠CMQ=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC=60°.
∴∠CMQ恒等于60°,不发生变化.
(2)设运动了t秒
当△PBQ为Rt三角形时 ∠B="60°"
①当∠BPQ=30°时 ∴PB="AB-BP=4-t=2BQ=2t" 解得t=![]()
②当∠PQB=30°时 则BQ=t=2PB=2(AB-AP)=2(4-t) 解得t=![]()
(3)∠CMQ不变.
∵AC=CB,∠ACQ=120°=∠CBP, CQ="BP,"
∴△ACQ≌△CBP, ∴∠CAQ=∠BCP,
∴∠CMQ=∠CAQ+∠ACM=∠BCP+∠ACM=∠MCQ+∠ACM=∠ACQ=120°.
∴∠CMQ恒等于120°,不会发生变化.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,D、E分别为△ABC的边AB、AC上点,BE与CD相交于点O.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.
(1)请你选出两个条件作为题设,余下作结论,写一个正确的命题:命题的条件是_______和_______,命题的结论是_______和________(均填序号)
(2)证明你写的命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 所有的等腰三角形都是锐角三角形
B. 等边三角形属于等腰三角形
C. 不存在既是钝角三角形又是等腰三角形的三角形
D. 一个三角形里有两个锐角,则一定是锐角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣2x2的图象如何移动,就得到y=﹣2x2+4x+1的图象( )
A.向左移动1个单位,向上移动3个单位
B.向左移动1个单位,向下移动3个单位
C.向右移动1个单位,向上移动3个单位
D.向右移动1个单位,向下移动3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
A. 明天太阳从东方升起
B. 任意画一个三角形,其内角和是360°
C. 通常温度降到0℃以下,纯净的水结冰
D. 射击运动员射击一次,命中靶心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A.同位角相等
B.有两边及一角分别相等的两个三角形全等
C.两组对边分别相等的四边形是平行四边形
D.垂直于半径的直线是圆的切线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com