
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点 为N(0,6),且与x轴交于A、B两点.
为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
解:(1)如图1,
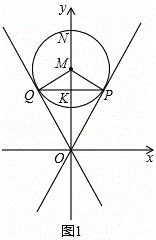
∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2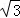 .
.
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=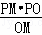 =
= =
=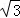 .
.
∴OK=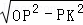 =3.
=3.
∴点P的坐标为(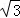 ,3).
,3).
(2)如图2,
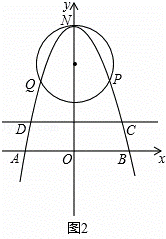
设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(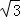 ,3)在抛物线y=ax2+6上,
,3)在抛物线y=ax2+6上,
∴3a+6=3.
解得:a=﹣1.
则该抛物线的解析式为y=﹣x2+6.
(3)当直线y=m与⊙M相切时,
则有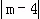 =2.
=2.
解得;m1=2,m2=6.
①m=2时,如图3,
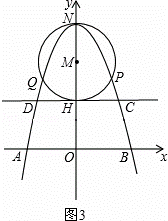
则有OH=2.
当y=2时,解方程﹣x2+6=2得:x=±2,
则点C(2,2),D(﹣2,2),CD=4.
同理可得:AB=2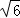 .
.
则S梯 形ABCD=(DC+AB)•OH=(4+2
形ABCD=(DC+AB)•OH=(4+2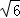 )×2=4+2
)×2=4+2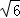 .
.
②m=6时,如图4,
此时点C、点D与点N重合.
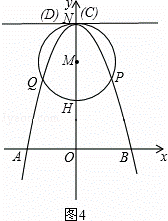
S△ABC=AB•OC=×2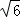 ×6=6
×6=6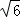 .
.
综上所述:点A、B、C、D围成的多边形的面积为4+2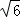 或6
或6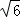 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
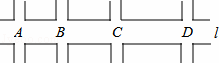
A. 50秒 B. 45秒 C. 40秒 D. 35秒
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所 示.
示.
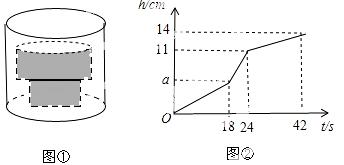
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 cm,匀速注水的水流速度为 cm3/s;
 (2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(﹣4,2)、B(﹣2,3)、C(﹣1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.
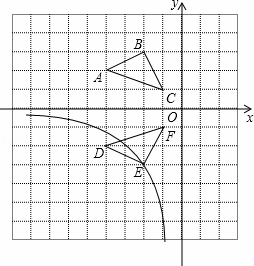
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,从一副普通扑克牌中选取红桃10、方块10、梅花5、黑桃8四张扑克牌,洗匀后正面朝下放在桌子上,甲先从中任意抽取一张后,乙再从剩余三张扑克牌中任意抽取一张,用画树形图或列表的方法,求甲、乙两人抽取的扑克牌的点数都是10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com