
 如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.若水面下降了2.5m,水面的宽度增加多少?
如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.若水面下降了2.5m,水面的宽度增加多少? 分析 根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=-2.5代入抛物线解析式得出水面宽度,即可得出答案.
解答 解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,把A点坐标(-2,0)代入得a=-0.5,
∴抛物线解析式为y=-0.5x2+2,
当水面下降2.5米,通过抛物线在图上的观察可转化为:
当y=-2.5时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,
可以通过把y=-2.5代入抛物线解析式得出: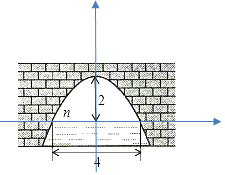
-2.5=-0.5x2+2,
解得:x=±3,(3分)
所以水面宽度增加到6米,比原先的宽度当然是增加了2米.
点评 此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,学会把实际问题转化为二次函数,利用二次函数的性质解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
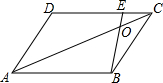 如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )
如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )| A. | 1:6 | B. | 1:9 | C. | 1:13 | D. | 1:12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的偏差(克) | -10 | -5 | 0 | +5 | +10 | +15 |
| 听数 | 2 | 5 | 4 | 6 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +3 | +4.5 | -2 | -2.5 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=13 | B. | (x+4)2=13 | C. | (x-4)2=11 | D. | (x-4)2=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com