
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒. 分析 先求出AB的长,再分①∠BDE=90°时,DE是△ABC的中位线,然后求出AE的长度,再分点E在AB上和在BA上两种情况列出方程求解即可;②∠BED=90°时,利用∠B的余弦列式求出BE,然后分点E在AB上和在BA上两种情况列出方程求解即可.
解答 解:∵∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=BC÷cos60°=4÷$\frac{1}{2}$=8,
①∠BDE=90°时,
∵D为BC的中点,
∴DE是△ABC的中位线,
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
点E在AB上时,t=4÷1=4秒;
②∠BED=90°时,BE=BD•cos60°=$\frac{1}{2}$×4×$\frac{1}{2}$=1,
点E在AB上时,t=(8-1)÷1=7,
综上所述,t的值为4或7.
故答案为:4或7.
点评 本题考查了三角形的中位线定理,解直角三角形,难点在于分情况讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:单选题
函数 ,自变量
,自变量 的取值范围是( )
的取值范围是( )
A. 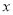 >3 B.
>3 B.  >-3 C.
>-3 C.  ≤-3 D.
≤-3 D.  ≥-3
≥-3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是大型输气管的截面图(圆形),某次数学实践活动中,数学课题学习小组为了计算大型输气管的直径,在圆形弧上取了A,B两点并连接AB,在劣弧AB上取中点C连接CB,经测量$BC=\frac{5}{4}$米,∠ABC=36.87°,请根据这些数据计算出大型输气管的直径(精确到0.1米).(sin36.87°≈0.60,cos36.87°≈0.80,tan36.87°≈0.75)
如图是大型输气管的截面图(圆形),某次数学实践活动中,数学课题学习小组为了计算大型输气管的直径,在圆形弧上取了A,B两点并连接AB,在劣弧AB上取中点C连接CB,经测量$BC=\frac{5}{4}$米,∠ABC=36.87°,请根据这些数据计算出大型输气管的直径(精确到0.1米).(sin36.87°≈0.60,cos36.87°≈0.80,tan36.87°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| X | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
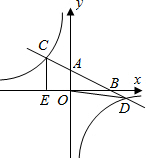 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
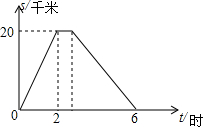 在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了$\frac{2}{3}$小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( )
在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了$\frac{2}{3}$小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD是一块绿化带,其中阴影部分EFGH是正方形花圃.一只小鸟随机落在绿化带区域内,则它停留在花圃上的概率是$\frac{2}{9}$.
如图,正方形ABCD是一块绿化带,其中阴影部分EFGH是正方形花圃.一只小鸟随机落在绿化带区域内,则它停留在花圃上的概率是$\frac{2}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com