
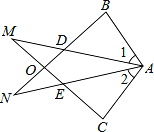
【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
【答案】(1)证明见解析(2)证明见解析
【解析】分析:(1)由SAS证明△ABD≌△ACE,得出对应边相等即可
(2)证出∠BAN=∠CAM,由全等三角形的性质得出∠B=∠C,由AAS证明△ACM≌△ABN,得出对应角相等即可.
本题解析:
(1)证明:在△ABD和△ACE中, 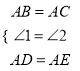 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)证明:∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM,
由(1)得:△ABD≌△ACE,
∴∠B=∠C,
在△ACM和△ABN中, 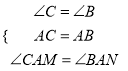 ,
,
∴△ACM≌△ABN(ASA),
∴∠M=∠N.
点睛:本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本的关键.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、白、黄3种颜色的若干个小球,它们除颜色外完全相同.每次从袋中摸出1个球,记下颜色后放回搅匀再摸.摸球实验中,统计得到下表中的数据:
摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
出现白球的频数 | 1 | 4 | 16 | 36 | 52 | 61 | 75 | 85 | 123 | 151 |
由此可以估计摸到黄球的概率约为________(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.
(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师对甲、乙两人的五次数学测验成绩进行统计,得出两人五次测验成绩的平均分均为90分,方差分别是S2甲=51、S2乙=12,由此可知( )
A. 甲比乙的成绩稳定B. 乙比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定D. 无法确定谁的成绩更稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com