Question

19．如图，竖立在点B处的标杆AB高2.5m，站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上．测得BD=9m，FB=3m，EF=1.7m，求树高CD．

Answer 1

分析 过E作EH⊥CD交CD于H点，交AB于点G，可证明四边形EFDH为长方形，可得HD的长；可证明△AEG∽△CEH，故可求得CH的长，所以树高CD的长即可知．

解答 解：过E作EH⊥CD交CD于H点，交AB于点G，如下图所示：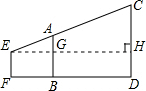
由已知得，EF⊥FD，AB⊥FD，CD⊥FD，
∵EH⊥CD，EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7，EG=FB=3，GH=BD=9
∴AG=AB-GB=0.8
∵EH⊥CD，EH⊥AB，
∴AG∥CH，
∴△AEG∽△CEH
∴$\frac{AG}{GH}=\frac{EG}{EH}$，
∵EH=EG+GH=12
∴CH=$\frac{AG×EH}{EG}$=3.2
∴CD=CH+HD=4.9
答：故树高DC为4.9米．

点评 本题考查了相似三角形在实际问题中的运用，关键是根据相似三角形的判定和性质进行解答．