
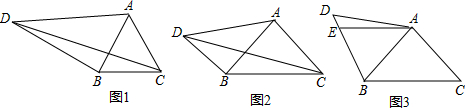
分析 (1)结论:DC2=DA2+DB2.如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.首先证明△DCM是等边三角形,再证明△ADM是直角三角形即可解决问题.
(2)①结论:DC2=DB2+2DA2.如图2中,作AM⊥AD交DB的延长线于M,连接CM.由△DAB≌△MAC,推出BD=CM,∠ADB=∠AMC=45°推出∠DMC=90°,推出DC2=CM2+DM2,由CM=DB,DM=$\sqrt{2}$AD,即可证明.
②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4-x,由AD=AM=5,推出DM=5$\sqrt{2}$,BM=DG=5$\sqrt{2}$-4,在Rt△DEG中,根据DG2+DE2=EG2,列出方程即可解决问题.
解答 解:(1)结论:DC2=DA2+DB2.
理由:如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.
∵CD=CM,∠DCM=60°,
∴△DCM是等边三角形,
∴DM=CD=CM,
∵∠ADB=30°,
∴∠DAB+∠DBA=150°,
∵∠MAC=∠DBC,
∴∠MAC+∠DAB=∠DBC+∠DAB=∠DBA+∠ABC+∠DAB=150°+60°=210°,
∴∠DAM=360°-210°-60°=90°,
∴DM2=DA2+AM2,∵AM=DB,DM=DC,
∴DC2=DA2+DB2.
故答案为DC2=DA2+DB2.
(2)①结论:DC2=DB2+2DA2.
理由:如图2中,作AM⊥AD交DB的延长线于M,连接CM.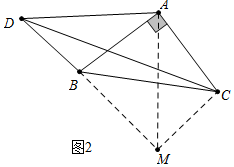
∵∠ADM=45°,∠DAM=90°,
∴∠ADM=∠AMD=45°,
∴DA=AM,DM=$\sqrt{2}$DA,
∵∠DAM=∠BAC,
∴∠DAB=∠MAC,∵AB=AC,
∴△DAB≌△MAC,
∴BD=CM,∠ADB=∠AMC=45°
∴∠DMC=90°,
∴DC2=CM2+DM2,
∵CM=DB,DM=$\sqrt{2}$AD,
∴DC2=DB2+2DA2.
②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.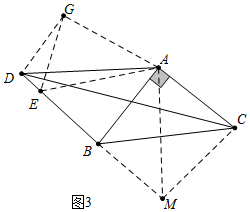
则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4-x,
∵AD=AM=5,
∴DM=5$\sqrt{2}$,BM=DG=5$\sqrt{2}$-4,
在Rt△DEG中,∵DG2+DE2=EG2,
∴(5$\sqrt{2}$-4)2+x2=(4-x)2,
解得x=$\frac{20\sqrt{2}-25}{4}$.
故答案为=$\frac{20\sqrt{2}-25}{4}$.
点评 本题考查时间最综合题、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线(旋转法),构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-3 | B. | x=-1 | C. | x=0 | D. | x=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
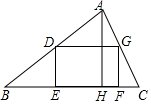 如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.
如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+y)(-x-y) | B. | (2a+b)(2a-b) | C. | (-3x-y)(-y+3x) | D. | (a2+b)(a2-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
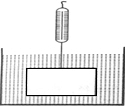 如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图象大致是( )
如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图象大致是( )| A. | 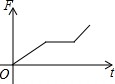 | B. | 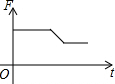 | C. | 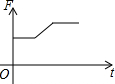 | D. | 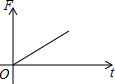 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com