
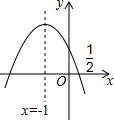 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号)
如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=-1,且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0.其中所有正确的结论是①③(填写序号) 分析 根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号及运用一些特殊点解答问题.
解答 解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以-$\frac{b}{2a}$=-1,可得b=2a,
a-2b+4c=a-4a+4c=-3a+4c,
∵a<0,
∴-3a>0,
∴-3a+4c>0,
即a-2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),
∴抛物线与x轴的另一个交点坐标为(-$\frac{5}{2}$,0),
当x=-$\frac{5}{2}$时,y=0,即a(-$\frac{5}{2}$)2-$\frac{5}{2}$b+c=0,
整理得:25a-10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴$\frac{1}{2}$b+b+c<0,
即3b+2c<0,故④错误;
故答案为:①③.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
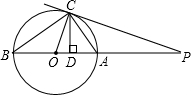 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com