
【题目】列方程组解应用题:用3辆![]() 型车和2辆
型车和2辆![]() 型车载满货物一次可运货17吨;用2辆
型车载满货物一次可运货17吨;用2辆![]() 型车和3辆
型车和3辆![]() 型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用
型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
(1)1辆![]() 型车和1辆
型车和1辆![]() 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?
(2)若![]() 型车每辆需租金200元/次,
型车每辆需租金200元/次,![]() 型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
【答案】(1)![]() :3
:3 ![]() :4;(2)选方案三
:4;(2)选方案三
【解析】
(1)根据“用3辆A型车和2辆B型车载满货物一次可运货17吨”“用2辆A型车和3辆B型车载满货物一次可运货18吨”,分别得出等式方程,组成方程组求出即可;
(2)由题意理解出:3a+4b=35,解此二元一次方程,求出其整数解,得到三种租车方案;利用A型车每辆需租金200元/次,B型车每辆需租金240元/次,分别求出租车费用即可.
(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:![]() ,
,
解方程组,得:![]() ,
,
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
(2)结合题意和(1)得:3a+4b=35,
∴a=![]()
∵a、b都是正整数
∴![]() 或
或![]() 或
或![]()
方案一:A型车9辆,B型车2辆;
方案二:A型车5辆,B型车5辆;
方案三:A型车1辆,B型车8辆.
∵A型车每辆需租金200元/次,B型车每辆需租金240元/次,
∴方案一需租金:9×200+2×240=2280(元)
方案二需租金:5×200+5×240=2200(元)
方案三需租金:1×200+8×240=2120(元)
∵2280>2200>2120
∴最省钱的租车方案是方案三:A型车1辆,B型车8辆,最少租车费为2120元.


科目:初中数学 来源: 题型:
【题目】某村的居民自来水管道需要改造.该工程若由甲队单独施工恰好在规定时间内完成,若乙队单独施工,则完成工程所需天数是规定天数的1.5倍,如果由甲、乙两队先合做![]() 天,那么余下的工程由甲队单独完成还需5天.设这项工程的规定时间是x天,则根据题意,下面所列方程正确的是( )
天,那么余下的工程由甲队单独完成还需5天.设这项工程的规定时间是x天,则根据题意,下面所列方程正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
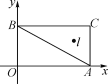
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
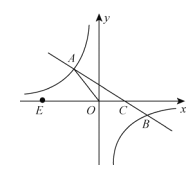
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
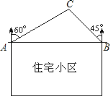
【题目】某住宅小区如图所示,小区东西两端的楼![]() 、
、![]() 之间的距离为
之间的距离为![]() ,某开发商准备在位于
,某开发商准备在位于![]() 楼的北偏东
楼的北偏东![]() 方向,且在
方向,且在![]() 楼的北偏西
楼的北偏西![]() 方向上的
方向上的![]() 处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆
处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆![]() 处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据
处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1.
(1)求证:∠ABE=∠CAD;
(2)求BP和AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
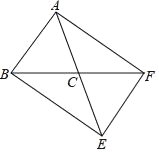
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
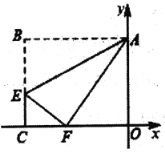
【题目】如图,在平面直角坐标系中,长方形![]() 的边
的边![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 在边
在边![]() 上,将该长方形沿
上,将该长方形沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,若
处,若![]() ,
,![]() ,则
,则![]() 所在直线的表达式为__________.
所在直线的表达式为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com