
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),
重合),![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .下列五个结论:①
.下列五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤若
;⑤若![]() ,则
,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
【答案】D
【解析】
试题解析:∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正确;
根据△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,∠COM=∠BON,
∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON,
又∵DO=CO,
∴△CON≌△DOM(SAS),故②正确;
∵∠BON+∠BOM=∠COM+∠BOM=90°,
∴∠MON=90°,即△MON是等腰直角三角形,
又∵△AOD是等腰直角三角形,
∴△OMN∽△OAD,故③正确;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故④正确;
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2﹣x,
∴△MNB的面积=![]() x(2﹣x)=﹣
x(2﹣x)=﹣![]() x2+x,
x2+x,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1﹣![]() =
=![]() ,故⑤正确;
,故⑤正确;
综上所述,正确结论的个数是5个,
故选:D.


科目:初中数学 来源: 题型:
【题目】如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2011个三角形,那么这个多边形是 ( )
A. 2012边形 B. 2013边形 C. 2014边形 D. 2015边形
查看答案和解析>>
科目:初中数学 来源: 题型:
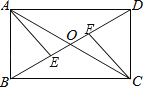
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 求证:四边形ADCE是菱形.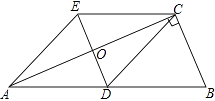
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F. 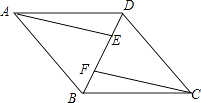
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com