练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20、用10个边长分别为3，5，6，11，17，19，22，23，24，25的正方形，可以拼接成一个矩形．
    （1）求这个矩形的长和宽；
    （2）请画出拼接图．
    分析：（1）根据已知条件求出10个正方形的面积，根据图形拼接前后图形面积不变即可求出矩形的长和宽，
    （2）根据矩形的对边相等，先拼出长方形的长，再拼出宽，即可画出拼接图．
    解答：解：（1）10个正方形的面积是32+52+62+112+172+192+222+232+242+252=3055=5×13×47，
    ∴拼成的长方形面积是3055，长方形的宽显然≥25，
    ∴它的宽应当是47，长应当是5×13=65；

    （2）根据23+24=47，25+22=47，即为长方形的宽，
    23+17+25=65，24+19+22=65，即为长方形的长，
    如图：
    点评：本题考查了图形拼接前后图形面积不变即可求矩形的长和宽；以及运用矩形的对边相等这一性质即可画出拼接图，难度较大．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
    例：在△ABC中，AB、BC、AC三边长分别是
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．
    小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：S△ABC=3×3-
    1
    2
    ×3×1-
    1
    2
    ×2×1-
    1
    2
    ×3×2=
    7
    2

    思维拓展：已知△ABC的边长分别为
    		5a
    、2
    		2a
    、
    		17a
    (a＞0)    ，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，用边长分别为1和3的两个正方形组成一个图形，则能将其完全覆盖的圆形纸片的最小半径为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•丹徒区模拟）用两个边长为1的正六边形拼接成如图（a）的图形，其周长为10；用三个边长为1的正六边形可以拼接成如图（b）或（c）的图形，其周长分别为12和14．若要拼接成周长为18的图形，所需这样的正六边形至少为x个，至多为y个，则x+y=
    11
    11
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

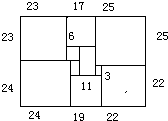
    如图所示，1925年数学家莫伦发现的世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形，其中标注（1）、（2）的正方形边长分别为x、y．
    请你计算：
    （1）第（4）个正方形的边长=
    x+2y
    x+2y
    ；第（8）个正方形的边长=
    7y-4x
    7y-4x
    ；第（10）个正方形的边长=
    3y-3x
    3y-3x
    ．（用含x、y的代数式表示）
    （2）当y=2时，第（6）个正方形的面积=
    64
    64
    ．

    查看答案和解析>>

    同步练习册答案