
����Ŀ��������10�֣���ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��y�ύ�ڵ�C����x�ύ�ڵ�B��������
��y�ύ�ڵ�C����x�ύ�ڵ�B��������![]() ����B��C���㣬��x��������ύ����һ��A����OA ��OC="2" ��7��
����B��C���㣬��x��������ύ����һ��A����OA ��OC="2" ��7��
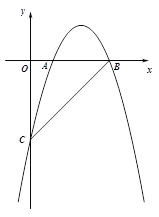


��1���������ߵĽ���ʽ��
��2����DΪ�߶�CB�ϣ���P�ڶԳ�����Ҳ��������ϣ�PD=PB����tan��PDB��������P������ꣻ
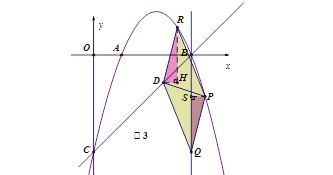
��3���ڣ�2���������£���Q��7��m���ڵ��������ڣ���R�ڶԳ�����Ҳ��������ϣ����Ե�P��D��Q��RΪ������ı���Ϊƽ���ı��Σ����Q��R�����꣮
���𰸡���1��y��-![]() x����
x����![]() x-7 ����2��P��8��-3����
x-7 ����2��P��8��-3����
��3��R��10��-12��,Q��7��-11����R��6��2����Q��7��-7��
�������������������1����ֱ�߽���ʽ�������C������꣬������OA ��OC="2" ��7�����A������.����A��C���������߽���ʽ�������.
��2�������B������ɵ���OCB=��OBC=45�����ֹ�P��PE��BC�ڵ�E��������CFG=��OCB==45���͵õ��߶�EF��BF��EP��������ϵ����tan��PDB�������Եõ��߶�EP��DE��PD��������ϵ��Ȼ�����P��F�������������ǵ���������ȼ������������ꣻ
��3�����Ե�P��D��Q��RΪ������ı���Ϊƽ���ı���������������߶�PD�п����DZ�Ҳ�п����ǶԽ���.
��PD�DZ�ʱ����DP��QRʱ����B��7��0����Q��7��n����BQ��y��
��P��PN��BQ����D��DN��BQ��PN�ڵ�N����R��RM��BQ�ڵ�M. ��PD��BQ�ڵ�T��DN��BM�ڵ�I
����֤����RMQ�ա�DNP�������D������꣬��R��ĺ�����Ϊt����RM=DN����t-7=8-5���t=10���ٰ�t=10���������������R��Q����PD�ǶԽ���ʱ��ͬ�����.
�����������1����ֱ��y=kx-7��y��ĸ����ύ�ڵ�C ��C��0��-7�� ��OC=7
��������y=ax2+bx+14a������C����14a=-7����a =-![]() ��y��-
��y��-![]() x����bx-7
x����bx-7
��OA ��OC="2" ��7����OA=2����A��2��0����������y��-![]() x����bx-7������A
x����bx-7������A
��b=![]() �������ߵĽ���ʽΪy��-
�������ߵĽ���ʽΪy��-![]() x����
x����![]() x-7
x-7

��2����ͼ1����������y��-![]() x����
x����![]() x-7����B�㣬 ��y=0���x=7��x=2���ᣩ��B��7��0��
x-7����B�㣬 ��y=0���x=7��x=2���ᣩ��B��7��0��
��OB=7��OC=OB���OCB=��OBC=45��
����P��PF��x���ڵ�G����CB�ӳ����ڵ�F��
��PF��y�ᣬ���CFG=��OCB==45��
��BF=![]() GF
GF
��P��PE��BC�ڵ�E��
��PD=PB
���PBD=��PDB
��tan��PBD=tan��PDB=2
��PE=2BE
��EF=PE ��BF=BE
��PF=![]() PE=2
PE=2![]() BE=2
BE=2![]() BF=4GF��
BF=4GF��
��PG="3GF"
��ֱ��y=kx-7��B�� ��k=1 ��y=x-7
��F��![]() ������P��
������P��![]() ��
��
����P��������y��-![]() x����
x����![]() x-7�ϣ�
x-7�ϣ�
���ԣ�![]()
���m=7���ᣩ��m=8
��P��8��-3��

��ͼ2,��DP��QRʱ�����ı���DQRP��ƽ���ı��� ��B��7��0����Q��7��n����BQ��y��
��P��PN��BQ����D��DN��BQ��PN�ڵ�N��
��R��RM��BQ�ڵ�M.
��PD��BQ�ڵ�T��DN��BM�ڵ�I
���DTB=��DPN����PTQ=��RQM, �ߡ�DTB=��PTQ
���DPN=��RQM
���ı���DPRQ��ƽ���ı���
��DP=RQ
�ߡ�RMQ=��DNP�����RMQ�ա�DNP
��RM=DN��MQ=PN
�ɣ�2������F��8��1����GF=1��BD=2BE=![]() BF=
BF=![]()
�ߡ�QBC=45������BI=DI=2 ��D��5��-2��
��R��ĺ�����Ϊt����RM=DN����t-7=8-5
���t=10
����R��������y��-![]() x����
x����![]() x-7 �ϣ�
x-7 �ϣ�
����t=10ʱ��![]()
��R��10,-12��
��MQ=PN
��3-2=-12-n����n=-11
��R��10��-12��,Q��7��-11��
��ͼ3����DR��QPʱ�����ı���DQPR��ƽ���ı���
ͬ�������R��6��2����Q��7��-7��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ��a��B��ʾ��b��C���ʾ��c��b����С������������a��b����![]() +(c��7)2=0��
+(c��7)2=0��
(1) a= ��b= ��c= ��
(2) ���������۵���ʹ��A����C���غϣ����B���� ��ʾ�ĵ��غϣ�
(3) ��A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����AB= ��AC= ��BC= ��(�ú�t�Ĵ���ʽ��ʾ)
(4) ���ʣ�3BC��2AB��ֵ�Ƿ�����ʱ��t�ı仯���ı�? ���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
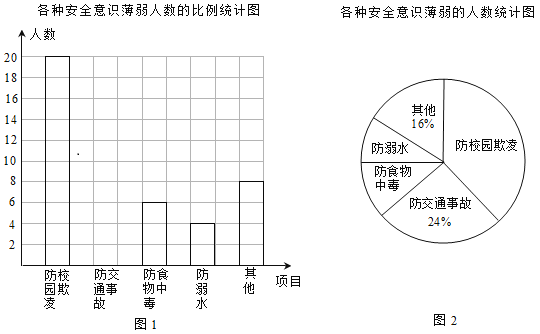
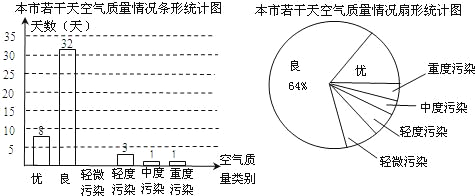
����Ŀ��ijУ��֯��һ�η���ˮ������ͨ�¹ʡ���ʳ���ж�����У���輰�������ְ�ȫ��ʶ�ĵ������˽�ͬѧ������Щ����İ�ȫ��ʶ���������ڽ����õؿ�չ��ȫ����������ݵ����������Ƴ�ͼ1��ͼ2������������ͳ��ͼ��
����ͼ�е���Ϣ����������⣺
(1)���ε��������Ϊ___________�����з�У������ʶ����������ռ_________%��
(2)��ȫ����ͳ��ͼ��
(3)����У����1500��ѧ��������Ƹ�Уѧ���з���ˮ��ʶ������������
(4)����������е���Ϣ������У�İ�ȫ������һ�������Ľ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ�������������ɫ��չ��̼���������٣�ij���г�����������һ����������Ͷ���г����ó�ԭ�ƻ�һ������1400������������ƽ��ÿ������200�������ڸ���ԭ��ʵ��ÿ����������ƻ�������г��룮�±���ij�ܵ��������������Ϊ��������Ϊ������

���Ÿ��ݼ�¼��֪ǰ���칲������ ������
���Ʋ�������һ��Ȳ������ٵ�һ��������� ������
���Ǹó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����ɵ�60Ԫ���������������������ÿ������15Ԫ��������һ����15Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��l1��ӳ��ij��˾����һ��ҽ����е����������(��Ԫ)��������(̨)֮��Ĺ�ϵ��l2��ӳ�˸ù�˾���۸���ҽ����е�����۳ɱ�(��Ԫ)��������(̨)֮��Ĺ�ϵ������������������۳ɱ�ʱ����ҽ����е�ſ�ʼӮ��������ͼ���������ж��д������( )
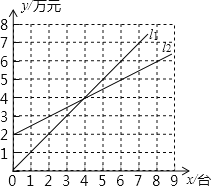
A. ��������Ϊ4̨ʱ���ù�˾Ӯ��4��Ԫ
B. ������������4̨ʱ���ù�˾�ſ�ʼӮ��
C. ��������Ϊ2̨ʱ���ù�˾����1��Ԫ
D. ��������Ϊ6̨ʱ���ù�˾Ӯ��1��Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��6��14������������Ѫ������ij�в�ȡ��Ը�����ķ�ʽ��֯����������Ѫ����ѪʱҪ����Ѫ�ߵ�Ѫ�ͽ��м�⣬���������A��������B��������AB��������O����4�����ͣ�����Ѫ����Ⱥ�У������ȡ�˲�����Ѫ�ߵ�Ѫ�ͽ������ͳ�ƣ����������ͳ�ƽ��������������������ͼ����
Ѫ�� | A | B | AB | O |
���� | �� �� | 10 | 5 | �� �� |
��1����������ȡ����Ѫ������Ϊ�� ���ˣ�m=�� ����
��2����ȫ�ϱ��е����ݣ�
��3������λ�и�����3000��������Ѫ��������ݳ�������ش�
����Ѫ����Ⱥ���γ�ȡһ�ˣ���Ѫ����A�͵ĸ����Ƕ��٣���������3000���д�Լ�ж�������A��Ѫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ�˽Ȿ�еĿ���������������л����������ȡ��������Ŀ������������Ϊ�걾����ͳ�ƣ����Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������ϢΪ������
�������ͼ���ṩ����Ϣ������������⣺
��1�����ε����й���ȡ�˶�����Ŀ������������Ϊ�걾��
��2��������Ⱦ��������ȫ����ͳ��ͼ��
��3��������Ƹ�����һ�꣨365�죩���������ﵽ������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϡ����������.
����ѭ��С��������
����֪������![]() д��С����ʽ��
д��С����ʽ��![]() ��������������ѭ��С��
��������������ѭ��С��![]() д�ɷ�����ʽ��
д�ɷ�����ʽ��![]() ��һ��أ��κ�һ������ѭ��С��������д�ɷ�����ʽ.
��һ��أ��κ�һ������ѭ��С��������д�ɷ�����ʽ.
��������ѭ��С��![]() Ϊ����������.
����������.
��![]() ����
����![]() ��֪��
��֪��![]() ������
������![]() ���ⷽ�̣���
���ⷽ�̣���![]() �����ǣ���
�����ǣ���![]() .
.
��������ѭ��С��![]() Ϊ��������һ��������.
Ϊ��������һ��������.
����ѭ��С��![]() ������ѭ��������λ�������������ۿ����뵽��������.
������ѭ��������λ�������������ۿ����뵽��������.
��![]() ����
����![]() ��֪��
��֪��![]() .
.
����![]() .�ⷽ�̣���
.�ⷽ�̣���![]() �����ǣ�
�����ǣ�![]() .
.
���Ӧ�ã�ֱ��д���𰸣���д���̣�
��![]() .��
.��![]() .��
.��![]() .
.
��������
��![]() ��Ϊ������ʽ��д������.
��Ϊ������ʽ��д������.
��չ̽��
��![]() ��
��
�ڱȽϴ�С![]() 1������
1������![]() ������
������![]() ������
������![]() ������
������
����![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90��������AB���е�OΪ����ԭ�㣬AB����ֱ��Ϊx�Ὠ����ƽ��ֱ������ϵ�У�����ABC�Ƶ�B˳ʱ����ת��ʹ��A��ת��y����������ϵ�A��������AO=OB=2������Ӱ�������Ϊ��������
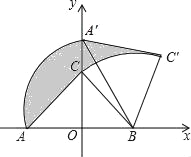
A. ![]() �� B.
�� B. ![]() ��1 C.
�Щ�1 C. ![]() +1 D.
+1 D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com