
【题目】又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)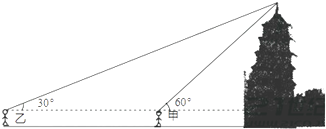
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,若大正方形的边长为a,小正方形的边长为b,则阴影部分的面积是 ;若如图中的阴影部分剪下来,重新拼叠成如图的一个矩形,则它长为 ;宽为 ;面积为 .
(2)由(1)可以得到一个公式: .
(3)利用你得到的公式计算:20192﹣2018×2020.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一条直线上依次有A、B、C三点.
(1)若BC=60,AC=3AB,求AB的长;
(2)若点D是射线CB上一点,点M为BD的中点,点N为CD的中点,求![]() 的值;
的值;
(3)当点P在线段BC的延长线上运动时,点E是AP中点,点F是BC中点,下列结论中:
①![]() 是定值;
是定值;
②![]() 是定值.其中只有一个结论是正确的,请选择正确结论并求出其值.
是定值.其中只有一个结论是正确的,请选择正确结论并求出其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
①将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
③直接写出点B2 , C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com