
【题目】如图,在平面直角坐标系中,直线y=![]() x+
x+![]() 与反比例函数y=
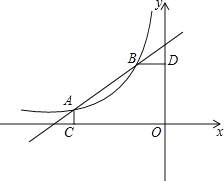
与反比例函数y=![]() (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(1)求a 、b及k的值;
(2)连接OA,OB,求△AOB的面积.
【答案】(1)a=![]() ,b=2,k= -2 ;(2)S△AOB =
,b=2,k= -2 ;(2)S△AOB =![]()
【解析】
(1)把A、B两点坐标代入直线解析式求出a,b的值,从而确定A、B两点坐标,再把A(或B)点坐标代入双曲线解析式求出k的值即可;
(2)设直线AB分别交x轴、y轴于点E,F,根据S△AOB=S△EOF-S△AEO-S△BFO求解即可.
(1)将点A(-4,a)、B(-1,b)分别代入表达式![]() 中,得:
中,得:
![]() ;
;![]() ,
,
∴A(-4,![]() )、B(-1,2)
)、B(-1,2)
将B(-1,2)代入y=![]() 中,得k=-2
中,得k=-2
所以a=![]() ,b=2,k= -2
,b=2,k= -2
(2)设直线AB分别交x轴、y轴于点E,F,如图,
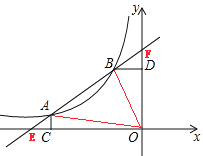
对于直线![]() ,分别令y=0,x=0,解得:
,分别令y=0,x=0,解得:
X=-5,y=![]() ,
,
∴E(-5,0),F(0,![]() )
)
由图可知:
S△AEO=![]() ×OE×AC=
×OE×AC=![]() ,S△BFO=
,S△BFO=![]() ×OF×BD=
×OF×BD=![]() ,
,
S△EOF=![]() ×OE×OF=
×OE×OF=![]()
∴S△AOB= S△EOF- S△AEO -S△BFO=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2, ![]() ,求线段DC的长;
,求线段DC的长;
(2)求证:EF·GB=BF·GE.

查看答案和解析>>
科目:初中数学 来源: 题型:
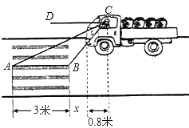
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
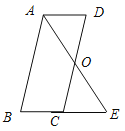
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
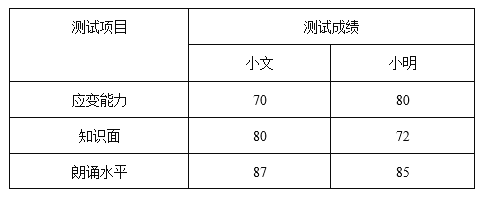
【题目】学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占x%,知识面占(50﹣x)%,其中0<x<50,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b互为相反数,m,n互为倒数,x的绝对值等于3,回答:
(1)由题目可得,a+b=_______ ,mn=_______ ,x=_______ ;
(2)求多项式2x2﹣(a+b+mn)x+(a+b)2017+(﹣mn)2017的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com