
【题目】如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( ) 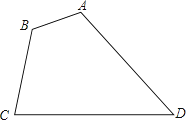
A.0<AD<7
B.2<AD<7
C.0<AD<13
D.1<AD<13
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为 . 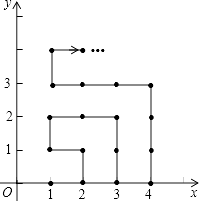
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: 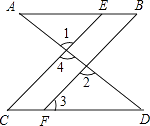
∵∠1=∠2(),
且∠1=∠4()
∴∠2=∠4(等量代换)
∴CE∥BF()
∴∠=∠3()
又∵∠B=∠C(已知)
∴∠3=∠B()
∴AB∥CD().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com