
王红和刘芳两人在玩转盘游戏,如图7,把转盘甲、乙分别分成3等份,并在每一份内标上数字,游戏规则是:转动两个转盘,停止后,指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜.那么这二人中获胜可能性较大的是_______.
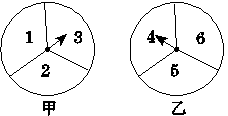
图7
科目:初中数学 来源: 题型:
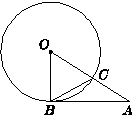
如图1,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )
A.40° B.50° C.65° D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图16,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
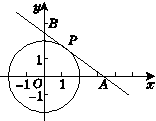
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在学习概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是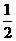 ”,小明做了下列三个模拟试验来验证.
”,小明做了下列三个模拟试验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图4),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值.
上面的试验中,不科学的有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图8).规定:同一日内,顾客在本商场每消费满100元就可以转转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得_______元购物券,最多可得______元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.

图8
查看答案和解析>>
科目:初中数学 来源: 题型:
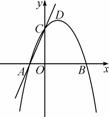
综合与探究:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点 D是该抛物线的顶点.
D是该抛物线的顶点.
(1)求直线AC的解析式及B、D两点的坐标;
(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q.试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形,若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;
(3 )请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
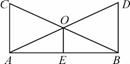
如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的关系 ,并给予证明.
,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com